
分析 运用双曲线的第二定义,可得双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上横坐标为$\frac{3a}{2}$的点到右焦点的距离=($\frac{3a}{2}$-$\frac{{a}^{2}}{c}$)e=$\frac{3c}{2}$-a,双曲线上横坐标为$\frac{3a}{2}$的点到左准线的距离=$\frac{3a}{2}$+$\frac{{a}^{2}}{c}$,由$\frac{3c}{2}$-a>$\frac{3a}{2}$+$\frac{{a}^{2}}{c}$,能够推导出双曲线离心率的取值范围是(2,+∞),即c>2a,进而得到a,b的关系,由渐近线的斜率,结合双曲线的渐近线的对称性,可得夹角的范围.
解答 解:双曲线的准线方程为x=±$\frac{{a}^{2}}{c}$,
由双曲线的第二定义,可得双曲线上横坐标为$\frac{3}{2}a$的点到右焦点的距离为:
e($\frac{3a}{2}$-$\frac{{a}^{2}}{c}$)=$\frac{c}{a}$•($\frac{3a}{2}$-$\frac{{a}^{2}}{c}$)=$\frac{3c}{2}$-a,
它到左准线的距离为$\frac{3a}{2}$+$\frac{{a}^{2}}{c}$,
即有$\frac{3c}{2}$-a>$\frac{3a}{2}$+$\frac{{a}^{2}}{c}$,
即为3c2-5ac-2a2>0,
同除以a2,可得3e2-5e-2>0,
解得e>2或e<-$\frac{1}{3}$(舍去).
即有c>2a,即c2>4a2,
即有a2+b2>4a2,
则b2>3a2,即有b>$\sqrt{3}$a,
而双曲线的渐近线的斜率为±$\frac{b}{a}$,
由$\frac{b}{a}$>$\sqrt{3}$,可得一条渐近线的倾斜角的范围为(60°,90°),
由对称性可得该双曲线两条渐近线所夹的锐角的取值范围是(0°,60°).
故答案为:(0°,60°).
点评 本题考查双曲线的第二定义和渐近线方程,以及对称性,解题的关键是准确把握双曲线上横坐标为$\frac{3a}{2}$的点到右焦点的距离,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{2}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {5} | B. | {0,5} | C. | {1,5} | D. | {0,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-6,+∞) | B. | [-6,+∞) | C. | (-∞,-6) | D. | (-∞,-6] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
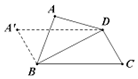 如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.
如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com