
分析 由题意可知{an}是等比数列,公比为2,求出a1即可得出an,Sn,从而得出Sn-2an的值.
解答 解:∵an+1=2an,∴{an}是以2为公比的等比数列,
∵a1+a3=$\frac{5}{8}$,∴a1+4a1=$\frac{5}{8}$,
解得a1=$\frac{1}{8}$,
∴an=$\frac{1}{8}×{2}^{n-1}$=2n-4,Sn=$\frac{\frac{1}{8}(1-{2}^{n})}{1-2}$=2n-3-$\frac{1}{8}$,
∴Sn-2an=2n-3-$\frac{1}{8}$-2n-3=-$\frac{1}{8}$.
故答案为:$-\frac{1}{8}$
点评 本题考查了等比数列的判断,等比数列的通项公式和求和公式,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
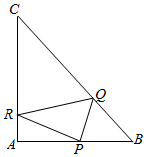 在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )
在等腰直角三角形ABC中,AB=AC=4,点P是边上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )| A. | 2 | B. | 1 | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
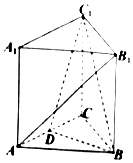 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )
如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )| A. | 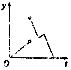 | B. | 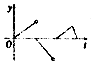 | C. | 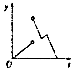 | D. | 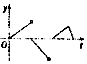 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com