练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知集合 ，
    （1）若 ，求 的取值范围；
    （2）若 ，求 的取值范围．

    【答案】
    （1）解： ，
    ， ，解得
    （2）解： ， 或 ，
    解得 或
    【解析】(1) 根据题意首先里一元二次不等式的解法取出集合A、B，再由子集的性质借助数轴得到关于a的不等式组，解出a的取值范围即可。(2)利用交集的性质结合题意，利用数轴即可求出a的取值范围。
    【考点精析】根据题目的已知条件，利用子集与真子集和集合的交集运算的相关知识可以得到问题的答案，需要掌握任何一个集合是它本身的子集；n个元素的子集有2n个,n个元素的真子集有2n －1个,n个元素的非空真子集有2n－2个；交集的性质：（1）A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在直角坐标平面内，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程是ρ=4sinθ，直线l的参数方程是 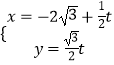（t为参数）．
    （1）求直线l的普通方程和曲线C的直角坐标方程；
    （2）求曲线C上的点到直线l的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着智能手机的发展，微信越来越成为人们交流的一种方式．某机构对使用微信交流的态度进行调查，随机调查了 50 人，他们年龄的频数分布及对使用微信交流赞成人数如表．

    年龄（岁）

    [15，25）

    [25，35）

    [35，45）

    [45，55）

    [55，65）

    [65，75）

    频数

    5

    10

    15

    10

    5

    5

    赞成人数

    5

    10

    12

    7

    2

    1

    （I）由以上统计数据填写下面 2×2 列联表，并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异；

    年龄不低于45岁的人

    年龄低于45岁的人

    合计

    赞成

    不赞成

    合计

    （Ⅱ）若对年龄在[55，65），[65，75）的被调查人中随机抽取两人进行追踪调查，记选中的4人中赞成使用微信交流的人数为X，求随机变量X的分布列和数学期望
    参考公式：K2= ，其中n=a+b+c+d
    参考数据：

    P（K2≥k0）

    0.050

    0.010

    0.001

    k0

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数y=f(x)的图象与g(x)=logax(a＞0，且a≠1)的图象关于x轴对称，且g(x)的图象过点(9,2)．
    （1）求函数f(x)的解析式；
    （2）若f(3x1)＞f(x＋5)成立，求x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P﹣ABCD中，底面ABCD是边长为1的正方形，PA⊥平面ABCD，PA=AB，M，N分别为PB，AC的中点，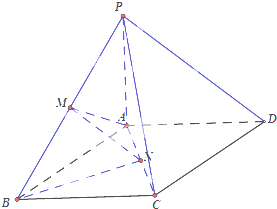
    （1）求证：MN∥平面PAD；
    （2）求点B到平面AMN的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，F1、F2分别是双曲线 ﹣ =1（a＞0，b＞0）的两个焦点，以坐标原点O为圆心，|OF1|为半径的圆与该双曲线左支交于A、B两点，若△F2AB是等边三角形，则双曲线的离心率为（ ）
    A.
    B.2
    C. ﹣1
    D.1+

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一条光线从点A(3,2)发出，经x轴反射后，通过点B(－1,6)，求入射光线和反射光线所在的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程，分别得到以下四个结论：
    ①y与x负相关且 ＝2.347x－6.423；②y与x负相关且 ＝－3.476x＋5.648；
    ③y与x正相关且 ＝5.437x＋8.493；④y与x正相关且 ＝－4.326x－4.578.
    其中一定不正确的结论的序号是( )
    A.①②
    B.②③
    C.③④
    D.①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设y1＝ ，y2＝ ，其中a>0，且a≠1，试确定x为何值时，有：
    （1）y1＝y2；
    （2）y1>y2.

    查看答案和解析>>

    同步练习册答案