Question

5．函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x，x≥1}\\{-x+1，x＜1}\end{array}\right.$，则满足方程f[f（m）]=log${\;}_{\frac{1}{2}}$f（m）的m的取值范围是（-∞，0]．

Answer 1

分析 通过m的取值，分类讨论方程是否有解，推出结果即可、

解答 解：当m≥1时，f（m）=$lo{g}_{\frac{1}{2}}m$＜0，
f[f（m）]=log${\;}_{\frac{1}{2}}$f（m）化为：-$lo{g}_{\frac{1}{2}}m$+1=$lo{g}_{\frac{1}{2}}（lo{g}_{\frac{1}{2}}m）$，无意义．
当m＜1时，f（m）=-m+1＞0，
①-m+1＜1，可得m∈（0，1），
方程f[f（m）]=log${\;}_{\frac{1}{2}}$f（m）有意义，
此时方程化为：-（-m+1）+1=$lo{g}_{\frac{1}{2}}（-m+1）$，
可得m=$lo{g}_{\frac{1}{2}}（-m+1）$，如图：方程无解．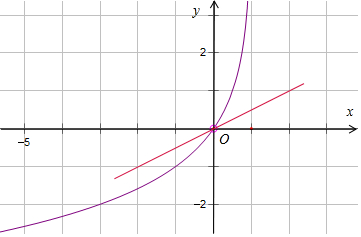

②当m≤0时，-m+1＞1，
方程化为：$lo{g}_{\frac{1}{2}}（-m+1）$═$lo{g}_{\frac{1}{2}}（-m+1）$，恒成立．
综上m的取值范围是：（-∞，0]．
故答案为：（-∞，0]．

点评 本题考查函数与方程的综合应用，考查数形结合分类讨论思想的应用，考查转化首项以及计算能力．