
| A. | [-1,1] | B. | (-1,1] | C. | [1,+∞) | D. | (-∞,-1) |
分析 根据分段函数的性质值域为R,具有连续性,x≥1时,f(x)=lnx是单调递增,则x<1时,f(x)=(a+1)x-2a也是递增.即可求实数a的范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{(a+1)x-2a,x<1}\\{lnx,x≥1}\end{array}\right.$的值域为R,
x≥1时,f(x)=lnx是单调递增,则x<1时,f(x)=(a+1)x-2a也是递增,
∴a+1>0,且(a+1)×1-2a≤ln1,
解得:-1<a≤1.
故得实数a的范围是(-1,1]
故选B.
点评 本题考查了分段函数的性质和值域的求法,单调性的运用.属于基础题.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:选择题
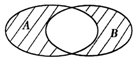 设函数f(x)=lg(1-x2),集合A为函数f(x)的定义域,集合B=(-∞,0]则图中阴影部分表示的集合为( )
设函数f(x)=lg(1-x2),集合A为函数f(x)的定义域,集合B=(-∞,0]则图中阴影部分表示的集合为( )| A. | [-1,0] | B. | (-1,0) | C. | (-∞,-1)∪[0,1) | D. | (-∞,-1]∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 99 | C. | 120 | D. | 121 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com