
【题目】已知 ![]() ,
, ![]() .
.
(1)求f(x)的解析式及定义域;
(2)求f(x)的值域;
(3)若方程f(x)=a2﹣3a+3有实数根,求实数a的取值范围.
【答案】
(1)解:设t=log3x,t∈[﹣1,1],则x=3t
f(t)=(3t)2﹣23t+4,
∴f(x)=(3x)2﹣23x+4,
f(x)的定义域为[﹣1,1]
(2)解:设u=3x, ![]() ,
,
f(u)=u2﹣2u+4=(u﹣1)2+3,
∴f(u)∈[3,7]
即所求值域为[3,7]
(3)解:由于方程f(x)=a2﹣3a+3有实数根,
∴a2﹣3a+3∈[3,7],
∴a∈[﹣1,0]∪[3,4]
【解析】(1)设t=log3x,得到t∈[﹣1,1],从而求出f(x)的解析式和函数的定义域即可;(2)设u=3x , 得到 ![]() ,求出f(u),从而求出函数的值域即可;(3)求出a2﹣3a+3∈[3,7],从而求出a的范围即可.
,求出f(u),从而求出函数的值域即可;(3)求出a2﹣3a+3∈[3,7],从而求出a的范围即可.
【考点精析】解答此题的关键在于理解函数的零点的相关知识,掌握函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率与双曲线
的离心率与双曲线![]() :
: ![]() 的离心率互为倒数,且经过点
的离心率互为倒数,且经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
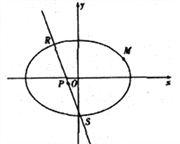
(2)如图,已知![]() 是椭圆上的两个点,线段
是椭圆上的两个点,线段![]() 的中垂线的斜率为
的中垂线的斜率为![]() 且与
且与![]() 交于点
交于点![]() ,
, ![]() 为坐标原点,求证:
为坐标原点,求证: ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把是BC上的△ABD折起,使∠BDC=90°.
(Ⅰ)证明:平面ADB⊥平面BDC;
(Ⅱ)设BD=1,求三棱锥D﹣ABC的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两种商品,经销这两种商品所能获得的利润分别是p万元和q万元.它们与投入资金x万元的关系是:p= ![]() x,q=
x,q= ![]() .今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获取最大利润?最大利润为多少?
.今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获取最大利润?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对一切x,y∈R都有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0.
(1)求f(0)的值;
(2)求f(x)的解析式;
(3)已知a∈R,设P:当 ![]() 时,不等式f(x)+3<2x+a恒成立,Q:当x∈[﹣2,2]时,g(x)=f(x)﹣ax是单调函数,如果记使P成立的实数a的取值的集合为A,使Q成立的实数a的取值的集合为B,求A∩RB.
时,不等式f(x)+3<2x+a恒成立,Q:当x∈[﹣2,2]时,g(x)=f(x)﹣ax是单调函数,如果记使P成立的实数a的取值的集合为A,使Q成立的实数a的取值的集合为B,求A∩RB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)满足以下条件:①定义在正实数集上;②f( ![]() )=2;③对任意实数t,都有f(xt)=tf(x)(x∈R+).
)=2;③对任意实数t,都有f(xt)=tf(x)(x∈R+).
(1)求f(1),f( ![]() )的值;
)的值;
(2)求证:对于任意x,y∈R+ , 都有f(xy)=f(x)+f(y);
(3)若不等式f(loga(x﹣3a)﹣1)﹣f(﹣ ![]()
![]() )≥﹣4对x∈[a+2,a+
)≥﹣4对x∈[a+2,a+ ![]() ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点M,N分别是正方体ABCD﹣A1B1C1D1的棱BB1和B1C1的中点,则MN和CD1所成角的大小为( )
A.30°
B.60°
C.90°
D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com