浙大优学小学年级衔接捷径浙江大学出版社系列答案科目：高中数学 来源： 题型：解答题
求下列各题中的函数f(x)的解析式．
(1) 已知f(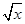
＋2)＝x＋4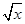，求f(x)；
(2) 已知f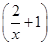
＝lgx，求f(x)；
(3) 已知函数y＝f(x)满足2f(x)＋f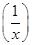
＝2x，x∈R且x≠0，求f(x)；
(4) 已知f(x)是二次函数，且满足f(0)＝1，f(x＋1)＝f(x)＋2x，求f(x)．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
（
为常数，且
）.
（1）当
时，求函数
的最小值（用表示）；
（2）是否存在不同的实数
使得
，
，并且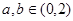
，若存在，求出实数的取值范围；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知定义域为R的函数f(x)=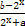
是奇函数.
(1)求a,b的值.
(2)用定义证明f(x)在(-∞,+∞)上为减函数.
(3)若对于任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
设函数f(x)＝
a为常数且a∈(0，1)．
(1)当a＝
时，求f
；
(2)若x0满足f[f(x0)]＝x0，但f(x0)≠x0，则称x0为f(x)的二阶周期点．证明函数f(x)有且仅有两个二阶周期点，并求二阶周期点x1，x2；
(3)对于(2)中的x1，x2，设A(x1，f[f(x1)])，B(x2，f[f(x2)])，C(a2，0)，记△ABC的面积为S(a)，求S(a)在区间[
，]上的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数
与听课时间
（单位：分钟）之间的关系满足如图所示的图像，当
时，图像是二次函数图像的一部分，其中顶点
，过点
；当
时，图像是线段
，其中
，根据专家研究，当注意力指数大于62时，学习效果最佳.
（1）试求
的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
的定义域为
，且的图象连续不间断. 若函数满足：对于给定的
（
且
），存在
，使得
，则称具有性质
.
（Ⅰ）已知函数
，
，判断是否具有性质
，并说明理由；
（Ⅱ）已知函数
若具有性质，求的最大值；
（Ⅲ）若函数的定义域为，且的图象连续不间断，又满足
，
求证：对任意
且
，函数具有性质
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
在区间(0，＋∞)上的单调性．
，其中
是常数．
时， 
是奇函数；
时，
的图像上不存在两点
、
，使得直线
平行于
轴．