
| A. | y=sin($\frac{x}{2}$+$\frac{π}{6}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=sin(2x-$\frac{π}{6}$) | D. | y=cos($\frac{x}{2}$-$\frac{π}{6}$) |
分析 由题意求出函数周期,可知满足条件的函数是选项B或C,再由在[-$\frac{π}{6}$,$\frac{π}{3}$]上是增函数进一步判断只有C符合.
解答 解:由图象的相邻两条对称轴间的距离是$\frac{π}{2}$,可知$\frac{T}{2}=\frac{π}{2}$,T=π,选项B、C满足.
由x∈[-$\frac{π}{6}$,$\frac{π}{3}$],得2x$+\frac{π}{3}$∈[0,π],函数y=cos(2x+$\frac{π}{3}$)为减函数,不合题意.
由x∈[-$\frac{π}{6}$,$\frac{π}{3}$],得2x-$\frac{π}{6}$∈[$\frac{π}{2}$,$\frac{π}{2}$],函数y=sin(2x-$\frac{π}{6}$)为增函数,符合合题意.
故选:C.
点评 本题考查三角函数的周期性及其求法,考查y=Asin(ωx+φ)型函数的图象和性质,是基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 | |
| B. | ?α,β∈R,使cos(α+β)=cosα+cosβ | |
| C. | 向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,0),则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为2 | |
| D. | “|x|≤1”是“x≤1”的既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
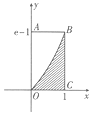 图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成,现向矩形区域OABC内随机投掷一点,则该点落在非阴影区域的概率是( )
图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成,现向矩形区域OABC内随机投掷一点,则该点落在非阴影区域的概率是( )| A. | $\frac{1}{e}$ | B. | $\frac{1}{e-1}$ | C. | 1-$\frac{1}{e}$ | D. | 1-$\frac{1}{e-1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或$\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5,6] | B. | (3,5) | C. | (3,6] | D. | [5,6] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com