
 已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x(1-x).
已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x(1-x).分析 (1)根据函数奇偶性的性质以及函数零点的定义进行求解即可.
(2)根据函数奇偶性的性质进行转化求解即可.
解答 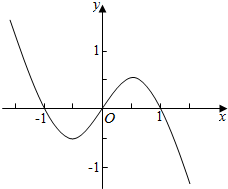 解:(1)当x≥0时,由f(x)=2x(1-x)=0得x=0或x=1,
解:(1)当x≥0时,由f(x)=2x(1-x)=0得x=0或x=1,
∵f(x)是定义在R上的奇函数,
∴当x<0时,函数的零点为-1,
即函数f(x)的零点为0,-1,1.
(2)若x<0,则-x>0,
∵x≥0时,f(x)=2x(1-x).
∴当-x>0时,f(-x)=-2x(1+x).
∵f(x)是定义在R上的奇函数,
∴f(-x)=-2x(1+x)=-f(x),
即f(x)=2x(1+x),x<0.
即f(x)=$\left\{\begin{array}{l}{2x(1-x),}&{x≥0}\\{2x(1+x),}&{x<0}\end{array}\right.$.
点评 本题主要考查函数零点的求解以及函数解析式的求解决,利用函数奇偶性的定义和性质进行转化是解决本题的关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:解答题
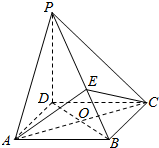 如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.
如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2,3) | B. | (-1,-2,3) | C. | (-1,2,-3) | D. | (-1,-2,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
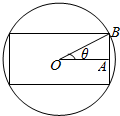 把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )
把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )| A. | y=50cos2θ | B. | y=25sinθ | C. | y=25sin2θ | D. | y=50sin2θ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{3}$-2,$\sqrt{3}$+2] | B. | [2-$\sqrt{3}$,2+$\sqrt{3}$] | C. | [0,2+$\sqrt{3}$] | D. | [0,2-$\sqrt{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com