练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．在正方体ABCD-A1B1C1D1中，E，F分别是BB1，CD的中点，求证D1F⊥平面ADE．

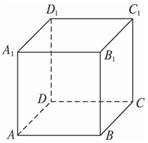
    分析 不妨设已知正方体的棱长为1个单位长度，建立空间直角坐标系D-xyz，利用向量数量积为0，证明线线垂直，从而证明线面垂直．

    解答 证明：不妨设已知正方体的棱长为1个单位长度，如图所示，建立空间直角坐标系D-xyz，
    则$\overrightarrow{AD}=（-1，0，0）$，$\overrightarrow{{D_1}F}=（0，\frac{1}{2}，-1）$，$\overrightarrow{AD}•\overrightarrow{{D_1}F}=（-1，0，0）•（0，\frac{1}{2}，-1）=0$，∴D1F⊥AD，
    又$\overrightarrow{AE}=（0，1，\frac{1}{2}）$，$\overrightarrow{AE}•\overrightarrow{{D_1}F}=（0，1，\frac{1}{2}）•（0，\frac{1}{2}，-1）=0$，
    ∴D1F⊥AE，AD∩AE=A，所以，D1F⊥平面ADE．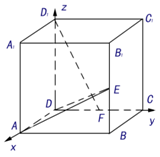

    点评 本题考查了空间线面位置关系，考查了向量法证明线面垂直，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．若直线x+y-2=0与直线x-y=0的交点P在角α的终边上，则tanα的值为（　　）
    A．1B．-1C．$\frac{1}{2}$D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．△ABC中，角A，B，C所对的边分别为a，b，c，acosC+ccosA=2bcosB．
    （1）求角B的值；
    （2）若a=4，b=6，求边c的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知f（x）=2x+1-eax（a∈R）．
    （1）讨论f（x）的单调性；
    （2）若x1，x2为方程f（x）=1的两个相异的实根，求证：x1+x2＞$\frac{2}{a}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设函数f（x）=6x3+3（a+2）x2+2ax．
    （I）若f（x）的两个极值点为x1，x2，且x1x2=1，求实数a的值；
    （II）是否存在实数a，使得f（x）是R上的单调函数？若存在，求出a的值，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知数列{an+81}是公比为3的等比数列，其中a1=-78，则数列{|an|}的前100项和为（　　）
    A．$\frac{{{3^{101}}-16203}}{2}$B．$\frac{{{3^{100}}-15387}}{2}$C．$\frac{{{3^{101}}-15387}}{2}$D．$\frac{{{3^{100}}-16203}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

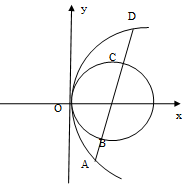    2．如右图抛物线顶点在原点，圆（x-2）2+y2=22的圆心恰是抛物线的焦点，
    （Ⅰ）求抛物线的方程；
    （Ⅱ）一直线的斜率等于2，且过抛物线焦点，它依次截抛物线和圆于A、B、C、D四点，求|AB|+|CD|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知等差数列{an}满足：a4＞0，a5＜0，则满足$\frac{{a}_{n+1}}{{a}_{n}}$＞2的n的集合是{5}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知x＞1，y＞1，且log2x，$\frac{1}{4}$，log2y成等比数列，则xy有（　　）
    A．最小值$\sqrt{2}$B．最小值2C．最大值$\sqrt{2}$D．最大值2

    查看答案和解析>>

    同步练习册答案