
若集合A1,A2,…,An满足A1∪A2∪…∪An=A,则称A1,A2,…,An为集合A的一种拆分.已知:
①当A1∪A2={a1,a2,a3}时,有33种拆分;
②当A1∪A2∪A3={a1,a2,a3,a4}时,有74种拆分;
③当A1∪A2∪A3∪A4={a1,a2,a3,a4,a5}时,有155种拆分;
……
由以上结论,推测出一般结论:
当A1∪A2∪…∪An={a1,a2,a3,…,an+1}时,有 种拆分.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
将1,2,3, ,9这9个正整数分别写在三张卡片上,要求每一张卡片上的任意两数之差都不在这张卡片上.现在第一张卡片上已经写有1和5,第二张卡片上写有2,第三张卡片上写有3,则6应该写在第 张卡片上;第三张卡片上的所有数组成的集合是 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
用数学归纳法证明 ≥
≥ n(a,b是非负实数,n∈N+)时,假设n
n(a,b是非负实数,n∈N+)时,假设n
=k命题成立之后,证明n=k+1命题也成立的关键是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
)在计算“1×2+2×3+…+n(n+1)”时,某同学学到了如下一种方法:先改写第k项:
k(k+1)=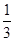 [k(k+1)(k+2)-(k-1)k(k+1)],
[k(k+1)(k+2)-(k-1)k(k+1)],
由此得1×2=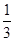 (1×2×3-0×1×2),
(1×2×3-0×1×2),
2×3=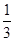 (2×3×4-1×2×3),…,
(2×3×4-1×2×3),…,
n(n+1)=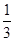 [n(n+1)(n+2)-(n-1)n(n+1)].
[n(n+1)(n+2)-(n-1)n(n+1)].
相加,得1×2+2×3+…+n(n+1)=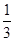 n(n+1)(n+2).
n(n+1)(n+2).
类比上述方法,请你计算“1×2×3+2×3×4+…+n(n+1)(n+2)”,其结果为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
观察下列等式: +
+ =1;
=1;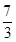 +
+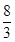 +
+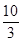 +
+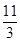 =12;
=12; +
+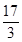 +
+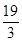 +
+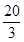 +
+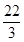 +
+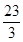 =39;
=39;
……
则当m<n且m,n∈N时,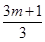 +
+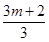 +
+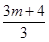 +
+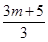 +…+
+…+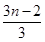 +
+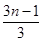 =________(最后结果用m,n表示).
=________(最后结果用m,n表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com