如图，三角形数阵满足：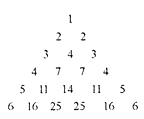
（1)第n行首尾两数均为n;
（2）表中的递推关系类似杨辉三角4则第n行（n≥2)第2个数是＿＿＿＿．
应用题天天练四川大学出版社系列答案科目：高中数学 来源： 题型：填空题
请阅读下列材料：若两个正实数a1，a2满足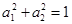
，那么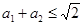
.
证明：构造函数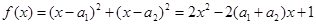
，因为对一切实数x，恒有
，所以 
，从而得
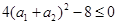，所以.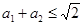
根据上述证明方法，若n个正实数满足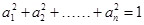
时，你能得到的结论为 .（不必证明）
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
观察下列等式:
(1+1)=2×1,
(2+1)(2+2)=22×1×3,
(3+1)(3+2)(3+3)=23×1×3×5,
……
照此规律,第n个等式可为 .
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
若集合A1,A2,…,An满足A1∪A2∪…∪An=A,则称A1,A2,…,An为集合A的一种拆分.已知:
①当A1∪A2={a1,a2,a3}时,有33种拆分;
②当A1∪A2∪A3={a1,a2,a3,a4}时,有74种拆分;
③当A1∪A2∪A3∪A4={a1,a2,a3,a4,a5}时,有155种拆分;
……
由以上结论,推测出一般结论:
当A1∪A2∪…∪An={a1,a2,a3,…,an+1}时,有 种拆分.
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
根据下面一组等式：
S1＝1；
S2＝2＋3＝5；
S3＝4＋5＋6＝15；
S4＝7＋8＋9＋10＝34；
S5＝11＋12＋13＋14＋15＝65；
S6＝16＋17＋18＋19＋20＋21＝111；
S7＝22＋23＋24＋25＋26＋27＋28＝175；
……
可得S1＋S3＋S5＋…＋S2n－1＝________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；第四行的第二个数可表示为
；第五行的第二个数可表示为
.….由此可合情推理，根据图形第n行的第二个数为
.故填
个图形是由正
边形拓展而来（
），则第
个图形共有____个顶点．
排在数表的第n行，第m列，则m＋n＝___________。
，
，
，……，由以上等式推测到一个一般的结论：对于n∈
，
；
=2
,
=3
,
=4
,…,若
=7
,(a,t均为正实数),则类比以上等式,可推测a、t的值,a+t= .