
分析 (1)由点P$({1,-\frac{{\sqrt{3}}}{2}})$在椭圆上,且离心率为$\frac{{\sqrt{3}}}{2}$,结合隐含条件列式求得a,b,则椭圆方程可求;
(2)当l的斜率不存在时,求出C,D的坐标,此时S1-S2=0;当l的斜率存在时,设l:y=k(x+$\sqrt{3}$)(k≠0),联立直线方程和椭圆方程,利用根与系数的关系把|S1-S2|转化为含有k的函数,利用基本不等式求最值,最后可得S1-S2的取值范围.
解答 解:(1)由已知得$\frac{1}{{a}^{2}}+\frac{3}{4{b}^{2}}=1$,①
又$\frac{c}{a}=\frac{\sqrt{3}}{2}$,∴$\frac{{c}^{2}}{{a}^{2}}=\frac{3}{4}$,即$\frac{{b}^{2}}{{a}^{2}}=\frac{1}{4}$,②
联立①、②解出a2=4,b2=1,
∴椭圆的方程是$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)当l的斜率不存在时,C($-\sqrt{3},-\frac{1}{2}$),D($-\sqrt{3},\frac{1}{2}$),此时S1-S2=0;
当l的斜率存在时,设l:y=k(x+$\sqrt{3}$)(k≠0),
设C(x1,y1),D(x2,y2),
联立$\left\{\begin{array}{l}{y=k(x+\sqrt{3})}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消y得$(4{k}^{2}+1){x}^{2}+8\sqrt{3}{k}^{2}x+(12{k}^{2}-4)=0$,
∴${x}_{1}+{x}_{2}=\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}},{x}_{1}{x}_{2}=\frac{12{k}^{2}-4}{1+4{k}^{2}}$.
∴|S1-S2|=2||y1|-|y2||=2|y1+y2|=2|k(x1+x2)+$2\sqrt{3}k$|=$\frac{4\sqrt{3}|k|}{4{k}^{2}+1}$,由于k≠0,
∴|S1-S2|=$\frac{4\sqrt{3}}{4|k|+\frac{1}{|k|}}$≤$\frac{4\sqrt{3}}{2\sqrt{4|k|•\frac{1}{|k|}}}=\sqrt{3}$,当且仅当4|k|=$\frac{1}{|k|}$时,即k=$±\frac{1}{2}$时,
|S1-S2|=$\sqrt{3}$,
∴S1-S2∈[-$\sqrt{3}$,$\sqrt{3}$].
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,训练了利用基本不等式求最值,是中档题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [1-$\sqrt{2}$,1+$\sqrt{2}$] | B. | [1-$\sqrt{2}$,3] | C. | [1-2$\sqrt{2}$,3] | D. | [-1,1+$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
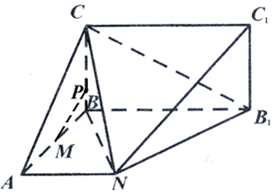 如图,已知平面ABB1N⊥平面BB1C1C,四边形BB1C1C,是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.
如图,已知平面ABB1N⊥平面BB1C1C,四边形BB1C1C,是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com