
A、
| ||
B、
| ||
C、
| ||
D、
|
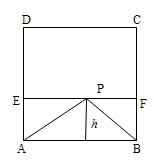 ∵正方形ABCD面积为9,∴正方形的边长AB=3.
∵正方形ABCD面积为9,∴正方形的边长AB=3.| 1 |
| 2 |
| 1 |
| 2 |


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
| an•bn |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、椭圆 |
| B、直线F1F2 |
| C、线段F1F2 |
| D、直线F1F2的垂直平分线 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 从学校参加数学竞赛的学生的试卷中抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘制频率分布直方图如图,从左至右各小组的小长方形的高之比为1:3:6:4:2,最右边一组的频数是6,请结合直方图提供的信息,解答下列问题:
从学校参加数学竞赛的学生的试卷中抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘制频率分布直方图如图,从左至右各小组的小长方形的高之比为1:3:6:4:2,最右边一组的频数是6,请结合直方图提供的信息,解答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:
| A、4 | B、3 | C、2 | D、1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com