
【题目】已知函数![]()
(1)若函数![]() 在区间
在区间![]() 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(2)若函数![]() 在区间
在区间![]() 上有两个极值点,求实数a的取值范围;
上有两个极值点,求实数a的取值范围;
(3)若函数![]() 的导函数
的导函数![]() 的图象与函数
的图象与函数![]() 图象有两个不同的交点,求实数a的取值范围.
图象有两个不同的交点,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)![]() 在区间
在区间![]() 上恒成立等价于当
上恒成立等价于当![]() 时,
时,![]() 恒成立,利用导数判断函数
恒成立,利用导数判断函数![]() 在
在![]() 上的单调性求出最大值即可得解;(2)求出导数,则
上的单调性求出最大值即可得解;(2)求出导数,则![]() 在区间
在区间![]() 上有两个不同零点,根据二次函数的图象与性质列出不等式组求a的取值范围,取
上有两个不同零点,根据二次函数的图象与性质列出不等式组求a的取值范围,取![]() ,
,![]() ,判断函数单调性验证
,判断函数单调性验证![]() ,
,![]() 分别为极大值与极小值即可;(3)题意等价于函数
分别为极大值与极小值即可;(3)题意等价于函数![]() 有两个零点,分析函数单调性知
有两个零点,分析函数单调性知![]() ,再根据
,再根据![]() 为函数
为函数![]() 的极值点即可代入不等式求出
的极值点即可代入不等式求出![]() 的范围从而求出a的范围,再验证函数
的范围从而求出a的范围,再验证函数![]() 的两个零点.
的两个零点.
(1)![]()
即当![]() 时,
时,![]() 恒成立,
恒成立,
设![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ,
,![]() .
.
(2)因为![]() ,
,
所以![]() 在区间
在区间![]() 上有两个极值点的必要条件为
上有两个极值点的必要条件为
![]() 在区间
在区间![]() 上有两个不同零点,
上有两个不同零点,
则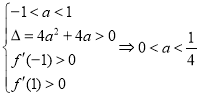 ,
,
当![]() 时,
时,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
![]() ,
,![]() ,
,![]()
所以存在唯一的![]() ,
,![]() 使得
使得![]() ,
,
因为![]() 在区间
在区间![]() 大于零,在区间
大于零,在区间![]() 小于零,在区间
小于零,在区间![]() 上大于零,
上大于零,
所以![]() 在区间
在区间![]() 上递增,在区间
上递增,在区间![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() ,
,![]() 分别为极大值与极小值,
分别为极大值与极小值,
所以当![]() 时函数
时函数![]() 在区间
在区间![]() 上有两个极值点;
上有两个极值点;
(3)因为![]()
所以![]() ,
,
令![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() (舍去),
(舍去),![]() .
.
|
|
|
|
|
| 0 | + |
| ↓ | 极小值 | ↑ |
因为![]() 有两个零点,
有两个零点,
所以![]() ,
,![]() ①
①
又因为![]() ,所以
,所以![]() ②
②
代入①得到![]() ,
,
令![]() ,
,![]()
所以![]() 在
在![]() 上递减,因为
上递减,因为![]() ,所以
,所以![]() ,
,
因为![]() 在区间
在区间![]() 上递增,所以
上递增,所以![]() .
.
i)因为![]() ,所以
,所以![]() ,
,
![]() ,
,
令![]() ,
,![]() ,
,
所以![]()
![]()
所以![]() 在
在![]() 上递增,
上递增,![]() ,所以
,所以![]()
所以![]() 在区间
在区间![]() 上存在唯一一个零点.
上存在唯一一个零点.
ⅱ)又因为![]()
![]()
![]() ,
,
且![]() ,
,
所以![]() 在区间
在区间![]() 上存在唯一一个零点,
上存在唯一一个零点,
综上![]() 时,
时,![]() 的图像与
的图像与![]() 图像有两个不同的交点.
图像有两个不同的交点.
解法二:由![]()
得![]()
令![]() ,
,
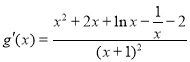
令![]() ,
,![]() .
.
![]() ,所以当
,所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在区间
在区间![]() 上递减,在区间
上递减,在区间![]() 上递增,
上递增,
所以![]() 即
即![]() ,
,
i)当![]() 时,因为
时,因为![]()
所以![]()
取![]() ,则
,则
![]()
所以![]() 在区间
在区间![]() 上存在唯一一个零点,
上存在唯一一个零点,
ii)当![]() 时,
时,
![]()
令![]() ,
,
![]()
因为![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 上递增,
上递增,
![]() ,所以
,所以![]() ,即
,即![]()
所以![]() 在区间
在区间![]() 上存在唯一一个零点,
上存在唯一一个零点,
综上![]() 时,
时,![]() 的图像与
的图像与![]() 图像有两个不同的交点.
图像有两个不同的交点.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}的前n项和为Sn,满足:对任意的n∈N*,都有an+1+Sn+1=1,又a1![]() .
.
(1)求数列{an}的通项公式;
(2)令bn=log2an,求![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在区间
在区间![]() 上有两个极值点
上有两个极值点![]() ,且
,且![]() 恒成立,求满足条件的
恒成立,求满足条件的![]() 的最小值(极值点是指函数取极值时对应的自变量的值).
的最小值(极值点是指函数取极值时对应的自变量的值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)当![]() 时,直线
时,直线![]() 被圆
被圆![]() 截得的弦长为__________;
截得的弦长为__________;
(2)若在圆![]() 上存在一点
上存在一点![]() ,在直线
,在直线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 的中点恰为坐标原点
的中点恰为坐标原点![]() ,则实数
,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC — A1B1C1中,AB=AC,BB1=BC,点P,Q,R分别是棱BC,CC1,B1C1的中点.
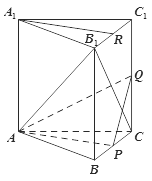
(1)求证:A1R//平面APQ;
(2)求证:直线B1C⊥平面APQ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:其中正确命题数是( )
A.在线性回归模型中,相关系数![]() 表示解释变量
表示解释变量![]() 对于预报变量
对于预报变量![]() 变化的贡献率,
变化的贡献率,![]() 越接近于1,表示回归效果越好
越接近于1,表示回归效果越好
B.两个变量相关性越强,则相关系数的绝对值就越接近于1
C.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位
平均减少0.5个单位
D.对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值来说,观测值越小,“
的观测值来说,观测值越小,“![]() 与
与![]() 有关系”的把握程度越大
有关系”的把握程度越大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情造成医用防护服紧缺,当地政府决定为防护服生产企业A公司扩大生产提供![]() (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到![]() (万件),其中k为工厂工人的复工率
(万件),其中k为工厂工人的复工率![]() ,A公司生产t万件防护服还需投入成本
,A公司生产t万件防护服还需投入成本![]() (万元).
(万元).
(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数;
(2)对任意的![]() (万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
(万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的左、右焦点分别为F1,F2,椭圆的焦距为2c,过C外一点P(c,2c)作线段PF1,PF2分别交椭圆C于点A、B,若|PA|=|AF1|,则
1(a>b>0)的左、右焦点分别为F1,F2,椭圆的焦距为2c,过C外一点P(c,2c)作线段PF1,PF2分别交椭圆C于点A、B,若|PA|=|AF1|,则![]() _____.
_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作![]() ,
,![]() 中,
中,![]() ,点
,点![]() ,点
,点![]() ,且其“欧拉线”与圆
,且其“欧拉线”与圆![]() 相切,则该圆的直径为( )
相切,则该圆的直径为( )
A.1B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com