
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“
是“![]() 数列”.
数列”.
(1)若![]() 是“
是“![]() 数列”,且
数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 是等差数列,首项为
是等差数列,首项为![]() ,公差为
,公差为![]() ,且
,且![]() ,判断
,判断![]() 是否为“
是否为“![]() 数列”;
数列”;
(3)设数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,若数列
,若数列![]() 与
与![]() 都是“
都是“![]() 数列”,求
数列”,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)见解析; (3)
; (2)见解析; (3)![]() .
.
【解析】
(1)根据数列的新定义,列出不等式组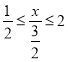 且
且![]() ,,即可求解;
,,即可求解;
(2)由等差数列![]() ,得到
,得到![]() ,进而得出
,进而得出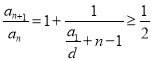 ,再由
,再由![]() 的单调性,得到
的单调性,得到![]() ,即可得到结论;
,即可得到结论;
(3)设等比数列![]() 的公比为
的公比为![]() ,分
,分![]() 和
和![]() 时,结合数列的新定义,即可作差判定.
时,结合数列的新定义,即可作差判定.
(1)由题意,数列![]() 满足
满足![]() ,称
,称![]() 是“
是“![]() 数列”,
数列”,
又由![]() ,
,![]() ,
,![]() ,
,![]() ,可得
,可得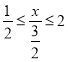 且
且![]() ,
,
解得![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(2)由题意,数列![]() 的通项公式为
的通项公式为![]() ,
,
则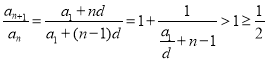 ,
,
又由![]() ,可得数列
,可得数列![]() 随着
随着![]() 的增大而减小,
的增大而减小,
所以当![]() 时,
时,![]() 取得最大值,所以
取得最大值,所以![]() ,
,
所以数列![]() 是“
是“![]() 数列”.
数列”.
(3)由题意得,等比数列![]() 的公比为
的公比为![]() ,
,
由数列![]() 是“G的数列”,可得
是“G的数列”,可得![]() ,即
,即![]() ,
,
①当![]() 时,所以
时,所以![]() ,则
,则![]() ,符合题意,
,符合题意,
②当![]() 时,则
时,则![]() ,则
,则![]() ,
,
因为数列![]() 是“G的数列”,所以
是“G的数列”,所以![]() 对
对![]() 恒成立,
恒成立,
(i)当![]() 时,
时,![]() ,
,
即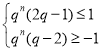 对
对![]() 恒成立,
恒成立,
因为![]() ,
,
所以![]() ,
,
所以当![]() 时,
时,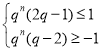 对
对![]() 恒成立;
恒成立;
(ii)当![]() 时,
时,![]() ,
,
即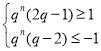 对
对![]() 恒成立,
恒成立,
因为![]() ,
,
所以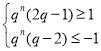 ,解得
,解得![]() ,
,
又![]() ,所以不存在
,所以不存在![]() 满足题意,
满足题意,
综上可得,数列![]() 的公比
的公比![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 是奇函数(其中
是奇函数(其中![]() )
)
(1)求实数m的值;
(2)已知关于x的方程![]() 在区间
在区间![]() 上有实数解,求实数k的取值范围;
上有实数解,求实数k的取值范围;
(3)当![]() 时,
时,![]() 的值域是
的值域是![]() ,求实数n与a的值.
,求实数n与a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(1)若![]() ,是否存在
,是否存在![]() ,有
,有![]() ?请说明理由;
?请说明理由;
(2)若![]() (
(![]() 、
、![]() 为常数,且
为常数,且![]() )对任意
)对任意![]() ,有
,有![]() ,试求出
,试求出![]() 、
、![]() 满足的充要条件;
满足的充要条件;
(3)若![]() ,
,![]() ,试确定所有
,试确定所有![]() ,使数列
,使数列![]() 中存在某个连续
中存在某个连续![]() 项的和是数列
项的和是数列![]() 中的一项,请证明.
中的一项,请证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 分别作射线
分别作射线![]() 、
、![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,且
,且![]() .试探究直线
.试探究直线![]() 是否过定点?如果是,请求出该定点;如果不是,请说明理由.
是否过定点?如果是,请求出该定点;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国际性会议纪念章的一特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向该会议的组织委员会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时,该店一年可销售2000枚,经过市场调研发现,每枚纪念章的销售价格在每枚20元的基础上,每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元(每枚的销售价格应为正整数).
元(每枚的销售价格应为正整数).
(1)写出该特许专营店一年内销售这种纪念章所获得的利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() 的函数关系式;
的函数关系式;
(2)当每枚纪念章销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出这个最大值;
(元)最大,并求出这个最大值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有![]() 多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的
多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的![]() 件工艺品测得重量(单位:
件工艺品测得重量(单位:![]() )数据如下表:
)数据如下表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
|
|
|
| |
|
| |
合计 |
|
(1)求出频率分布表中实数![]() ,
,![]() 的值;
的值;
(2)若从仿制的![]() 件工艺品重量范围在
件工艺品重量范围在![]() 的工艺品中随机抽选
的工艺品中随机抽选![]() 件,求被抽选
件,求被抽选![]() 件工艺品重量均在范围
件工艺品重量均在范围![]() 中的概率.
中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com