解:(Ⅰ)函数f(x)的定义域为(0,+∞),f′(x)=(ax+lnx)′=a+

,
①当a=0时,f′(x)>0,∴f(x)在(0,+∞)为单调递增函数;
②当a<0时,f′(x)=0,得x=-

,当x∈(0,-

)时,f′(x)>0;当x∈(-

,+∞)时,f′(x)<0;
∴f(x)在(0,-

)为单调递增函数;在(-

,+∞)为单调递减函数;
(II)由题意,不等式g(x)<
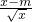
有解,即
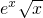
<x-m有解,
因此只须m<x-
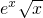
,x∈(0,+∞),
设h(x)=x-
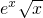
,x∈(0,+∞),h′(x)=1-e
x(

+
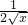
),
因为
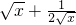
≥2
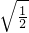
=

>1,且e
x>1,∴1-e
x(
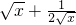
)<0,
故h(x)在(0,+∞)上是减函数,
∴h(x)<h(0)=0,故m<0.
(III)当a=0时,f(x)=lnx,f(x)与g(x)的公共定义域为(0,+∞),
|f(x)-g(x)|=|lnx-e
x|=e
x-lnx=e
x-x-(lnx-x),
设m(x)=e
x-x,x∈(0,+∞),
因为m′(x)=e
x-1>0,m(x)在(0,+∞)上是增函数,m(x)>m(0)=1,
又设n(x)=lnx-x,x∈(0,+∞),
因为n′(x)=

-1,当x∈(0,1)时,n′(x)>0,n(x)在(0,1)上是增函数,
当x∈(1,+∞)时,n′(x)<0,n(x)在(1.+∞)上是减函数,
∴当x=1时,n(x)取得极大值,即n(x)≤n(1)=-1,
故|f(x)-g(x)|=m(x)-n(x)>1-(-1)=2.
分析:(Ⅰ)先求出其导函数,以及导函数大于0,小于0对应的区间即可求函数f(x)的单调区间;
(II)因为关于x的不等式g(x)<
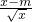
有解,将问题转化为
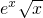
<x-m有解,利用分离常数法进行求解;
(III)当a=0时,f(x)=lnx,f(x)与g(x)的公共定义域为(0,+∞),由于|f(x)-g(x)|=|lnx-e
x|=e
x-lnx=e
x-x-(lnx-x),设m(x)=e
x-x,利用导数研究其单调性得出m(x)>m(0)=1,同样地,设n(x)=lnx-x,x∈(0,+∞),得到n(x)≤n(1)=-1,从而有|f(x)-g(x)|=m(x)-n(x)>1-(-1)=2;
点评:本题考查利用导数求函数的单调区间的方法,求函数的导数以及利用导数研究函数的极值.注意函数的定义域,此题是一道综合性题,考查学生计算能力;

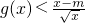 有解,求实数m的取值菹围;
有解,求实数m的取值菹围; ,
, ,当x∈(0,-
,当x∈(0,- )时,f′(x)>0;当x∈(-
)时,f′(x)>0;当x∈(- ,+∞)时,f′(x)<0;
,+∞)时,f′(x)<0; )为单调递增函数;在(-
)为单调递增函数;在(- ,+∞)为单调递减函数;
,+∞)为单调递减函数;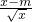 有解,即
有解,即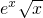 <x-m有解,
<x-m有解,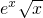 ,x∈(0,+∞),
,x∈(0,+∞),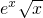 ,x∈(0,+∞),h′(x)=1-ex(
,x∈(0,+∞),h′(x)=1-ex( +
+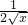 ),
),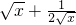 ≥2
≥2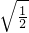 =
= >1,且ex>1,∴1-ex(
>1,且ex>1,∴1-ex(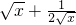 )<0,
)<0, -1,当x∈(0,1)时,n′(x)>0,n(x)在(0,1)上是增函数,
-1,当x∈(0,1)时,n′(x)>0,n(x)在(0,1)上是增函数,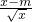 有解,将问题转化为
有解,将问题转化为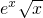 <x-m有解,利用分离常数法进行求解;
<x-m有解,利用分离常数法进行求解;

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案