
【题目】某同学用“随机模拟方法”计算曲线![]() 与直线
与直线![]() 所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[1,e]上的均匀随机数xi和10个在区间[0,1]上的均匀随机数
所围成的曲边三角形的面积时,用计算机分别产生了10个在区间[1,e]上的均匀随机数xi和10个在区间[0,1]上的均匀随机数![]()
![]() ,其数据如下表的前两行.
,其数据如下表的前两行.
x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
lnx | 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得这个曲边三角形面积的一个近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】东方商店欲购进某种食品(保质期两天),此商店每两天购进该食品一次(购进时,该食品为刚生产的).根据市场调查,该食品每份进价![]() 元,售价
元,售价![]() 元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响,为了了解市场的需求情况,现统计该产品在本地区
元,如果两天内无法售出,则食品过期作废,且两天内的销售情况互不影响,为了了解市场的需求情况,现统计该产品在本地区![]() 天的销售量如下表:
天的销售量如下表:

(视样本频率为概率)
(1)根据该产品![]() 天的销售量统计表,记两天中一共销售该食品份数为
天的销售量统计表,记两天中一共销售该食品份数为![]() ,求
,求![]() 的分布列与期望
的分布列与期望
(2)以两天内该产品所获得的利润期望为决策依据,东方商店一次性购进![]() 或
或![]() 份,哪一种得到的利润更大?
份,哪一种得到的利润更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着自媒体直播平台的迅猛发展,直播平台上涌现了许多知名三农领域创作者,通过直播或视频播放,帮助当地农民在直播平台上销售了大量的农产品,促进了农村的经济发展,当地农业与农村管理部门对近几年的某农产品年产量进行了调查,形成统计表如下:
年份 |
|
|
|
|
|
|
年份代码 |
|
|
|
|
|
|
年产量 |
|
|
|
|
|
|
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测![]() 年该地区该农产品的年产量;
年该地区该农产品的年产量;
(3)从![]() 年到
年到![]() 年的
年的![]() 年年产量中随机选出
年年产量中随机选出![]() 年的产量进行具体调查,求选出的
年的产量进行具体调查,求选出的![]() 年中恰有一年的产量小于
年中恰有一年的产量小于![]() 万吨的概率.
万吨的概率.
附:对于一组数据![]() 、
、![]() 、
、![]() 、
、![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .(参考数据:
.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且内切于圆
的离心率互为倒数,且内切于圆![]() .
.
(1)求椭圆M的方程;
(2)已知R![]() 是椭圆M上的一动点,从原点O引圆R:
是椭圆M上的一动点,从原点O引圆R:![]() 的两条切线,分别交椭圆M于P、Q两点,直线OP与直线OQ的斜率分别为
的两条切线,分别交椭圆M于P、Q两点,直线OP与直线OQ的斜率分别为![]() ,试探究
,试探究![]() 是否为定值并证明你所探究出的结论.
是否为定值并证明你所探究出的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,使得平面
同侧折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得到图2.
,得到图2.
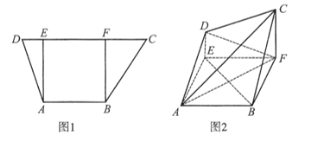
(1)证明:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com