
ЎҫМвДҝЎҝЛжЧЕЧФГҪМеЦұІҘЖҪМЁөДСёГН·ўХ№Ј¬ЦұІҘЖҪМЁЙПУҝПЦБЛРн¶аЦӘГыИэЕ©БмУтҙҙЧчХЯЈ¬НЁ№эЦұІҘ»тКУЖөІҘ·ЕЈ¬°пЦъөұөШЕ©ГсФЪЦұІҘЖҪМЁЙППъКЫБЛҙуБҝөДЕ©ІъЖ·Ј¬ҙЩҪшБЛЕ©ҙеөДҫӯјГ·ўХ№Ј¬өұөШЕ©ТөУлЕ©ҙе№ЬАнІҝГЕ¶ФҪьјёДкөДДіЕ©ІъЖ·ДкІъБҝҪшРРБЛөчІйЈ¬РОіЙНіјЖұнИзПВЈә
Дк·Э |
|
|
|
|
|
|
Дк·ЭҙъВл |
|
|
|
|
|
|
ДкІъБҝ |
|
|
|
|
|
|
ЈЁ1Ј©ёщҫЭұнЦРКэҫЭЈ¬ҪЁБў![]() №ШУЪ
№ШУЪ![]() өДПЯРФ»Ш№й·ҪіМ
өДПЯРФ»Ш№й·ҪіМ![]() Ј»
Ј»
ЈЁ2Ј©ёщҫЭПЯРФ»Ш№й·ҪіМФӨІв![]() ДкёГөШЗшёГЕ©ІъЖ·өДДкІъБҝЈ»
ДкёГөШЗшёГЕ©ІъЖ·өДДкІъБҝЈ»
ЈЁ3Ј©ҙУ![]() ДкөҪ
ДкөҪ![]() ДкөД
ДкөД![]() ДкДкІъБҝЦРЛж»ъСЎіц
ДкДкІъБҝЦРЛж»ъСЎіц![]() ДкөДІъБҝҪшРРҫЯМеөчІйЈ¬ЗуСЎіцөД
ДкөДІъБҝҪшРРҫЯМеөчІйЈ¬ЗуСЎіцөД![]() ДкЦРЗЎУРТ»ДкөДІъБҝРЎУЪ
ДкЦРЗЎУРТ»ДкөДІъБҝРЎУЪ![]() Нт¶ЦөДёЕВК.
Нт¶ЦөДёЕВК.
ёҪЈә¶ФУЪТ»ЧйКэҫЭ![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ј¬Жд»Ш№йЦұПЯ
Ј¬Жд»Ш№йЦұПЯ![]() өДРұВКәНҪШҫаөДЧоРЎ¶юіЛ№АјЖ·ЦұрОӘ
өДРұВКәНҪШҫаөДЧоРЎ¶юіЛ№АјЖ·ЦұрОӘ Ј¬
Ј¬![]() Ј®ЈЁІОҝјКэҫЭЈә
Ј®ЈЁІОҝјКэҫЭЈә![]() Ј©
Ј©
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©ФӨІв
Ј»ЈЁ2Ј©ФӨІв![]() ДкёГөШЗшёГЕ©ІъЖ·өДДкІъБҝФјОӘ
ДкёГөШЗшёГЕ©ІъЖ·өДДкІъБҝФјОӘ![]() Нт¶ЦЈ»ЈЁ3Ј©
Нт¶ЦЈ»ЈЁ3Ј©![]() .
.
ЎҫҪвОцЎҝ
ЈЁ1Ј©јЖЛгіц![]() әН
әН![]() Ј¬И»әуҪ«ұнёсЦРөДКэҫЭҙъИлЧоРЎ¶юіЛ·Ё№«КҪЗуіц
Ј¬И»әуҪ«ұнёсЦРөДКэҫЭҙъИлЧоРЎ¶юіЛ·Ё№«КҪЗуіц![]() әН
әН![]() өДЦөЈ¬јҙҝЙөГіц»Ш№йЦұПЯөД·ҪіМЈ»
өДЦөЈ¬јҙҝЙөГіц»Ш№йЦұПЯөД·ҪіМЈ»
ЈЁ2Ј©Ҫ«![]() ҙъИл»Ш№йЦұПЯ·ҪіМЈ¬јЖЛгіц
ҙъИл»Ш№йЦұПЯ·ҪіМЈ¬јЖЛгіц![]() өДЦөЈ¬јҙҝЙФӨІвіц
өДЦөЈ¬јҙҝЙФӨІвіц![]() ДкёГөШЗшёГЕ©ІъЖ·өДДкІъБҝЈ»
ДкёГөШЗшёГЕ©ІъЖ·өДДкІъБҝЈ»
ЈЁ3Ј©јЗКВјю![]() Ў°
Ў°![]() ДкөДІъБҝЦРЗЎУРТ»ДкөДІъБҝөНУЪ
ДкөДІъБҝЦРЗЎУРТ»ДкөДІъБҝөНУЪ![]() Нт¶ЦЎұЈ¬БРҫЩіцЛщУРөД»щұҫКВјюЈ¬ІўИ·¶ЁКВјю
Нт¶ЦЎұЈ¬БРҫЩіцЛщУРөД»щұҫКВјюЈ¬ІўИ·¶ЁКВјю![]() Лщ°ьә¬өД»щұҫКВјюКэЈ¬АыУГ№ЕөдёЕРНөДёЕВК№«КҪјҙҝЙјЖЛгіцКВјю
Лщ°ьә¬өД»щұҫКВјюКэЈ¬АыУГ№ЕөдёЕРНөДёЕВК№«КҪјҙҝЙјЖЛгіцКВјю![]() өДёЕВК.
өДёЕВК.
ЈЁ1Ј©УЙМвТвҝЙЦӘЈә![]() Ј¬
Ј¬![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
 Ј¬
Ј¬![]() Ј¬
Ј¬
![]() №ШУЪ
№ШУЪ![]() өДПЯРФ»Ш№й·ҪіМОӘ
өДПЯРФ»Ш№й·ҪіМОӘ![]() Ј»
Ј»
ЈЁ2Ј©УЙЈЁ1Ј©ҝЙөГЈ¬өұДк·ЭОӘ![]() ДкКұЈ¬Дк·ЭҙъВл
ДкКұЈ¬Дк·ЭҙъВл![]() Ј¬ҙЛКұ
Ј¬ҙЛКұ![]() Ј¬
Ј¬
ЛщТФҝЙФӨІв![]() ДкёГөШЗшёГЕ©ІъЖ·өДДкІъБҝФјОӘ
ДкёГөШЗшёГЕ©ІъЖ·өДДкІъБҝФјОӘ![]() Нт¶ЦЈ»
Нт¶ЦЈ»
ЈЁ3Ј©УЙМвЦӘЈ¬ЛщУРөД»щұҫКВјюУРЈә![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ўў
Ўў![]() Ј¬№І
Ј¬№І![]() ёцЈ¬
ёцЈ¬
ЙиКВјю![]() Ў°
Ў°![]() ДкөДІъБҝЦРЗЎУРТ»ДкөДІъБҝөНУЪ
ДкөДІъБҝЦРЗЎУРТ»ДкөДІъБҝөНУЪ![]() Нт¶ЦЎұЈ¬Фт
Нт¶ЦЎұЈ¬Фт![]() ЦРУР
ЦРУР![]() ёц»щұҫКВјюЈ¬№К
ёц»щұҫКВјюЈ¬№К![]() .
.



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ![]() КЗ¶ЁТеФЪ
КЗ¶ЁТеФЪ![]() ЙПөДәҜКэЈ¬јЗ
ЙПөДәҜКэЈ¬јЗ![]() Ј¬
Ј¬![]() өДЧоҙуЦөОӘ
өДЧоҙуЦөОӘ![]() .ИфҙжФЪ
.ИфҙжФЪ![]() Ј¬ВъЧг
Ј¬ВъЧг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬ФтіЖТ»ҙОәҜКэ
Ј¬ФтіЖТ»ҙОәҜКэ![]() КЗ
КЗ![]() өДЎ°ұЖҪьәҜКэЎұҙЛКұөД
өДЎ°ұЖҪьәҜКэЎұҙЛКұөД![]() іЖОӘ
іЖОӘ![]() ФЪ
ФЪ![]() ЙПөДЎ°ұЖҪьИ·ҪзЎұ.
ЙПөДЎ°ұЖҪьИ·ҪзЎұ.
ЈЁ1Ј©СйЦӨ![]() КЗ
КЗ![]() Ј¬
Ј¬![]() өДЎ°ұЖҪьәҜКэЎұЈ»
өДЎ°ұЖҪьәҜКэЎұЈ»
ЈЁ2Ј©ТСЦӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .Иф
.Иф![]() КЗ
КЗ![]() өДЎ°ұЖҪьәҜКэЎұЈ¬ЗуaЈ¬bөДЦөЈ»
өДЎ°ұЖҪьәҜКэЎұЈ¬ЗуaЈ¬bөДЦөЈ»
ЈЁ3Ј©ТСЦӘ![]() Ј¬
Ј¬![]() Ј¬ЗуЦӨЈ»¶ФИОТвіЈКэaЈ¬bЈ¬
Ј¬ЗуЦӨЈ»¶ФИОТвіЈКэaЈ¬bЈ¬![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝУРБҪЦЦАнІЖІъЖ·![]() әН
әН![]() Ј¬Н¶ЧКХвБҪЦЦАнІЖІъЖ·Т»ДкәуУҜҝчөДЗйҝцИзПВЈЁГҝЦЦАнІЖІъЖ·өДІ»Н¬Н¶ЧКҪб№ыЦ®јдПа»Ҙ¶АБўЈ©Јә
Ј¬Н¶ЧКХвБҪЦЦАнІЖІъЖ·Т»ДкәуУҜҝчөДЗйҝцИзПВЈЁГҝЦЦАнІЖІъЖ·өДІ»Н¬Н¶ЧКҪб№ыЦ®јдПа»Ҙ¶АБўЈ©Јә
ІъЖ·![]() Јә
Јә
Н¶ЧКҪб№ы | »сАы | І»ЕвІ»Ч¬ | ҝчЛр |
ёЕВК |
|
|
|
ІъЖ·![]() Јә
Јә
Н¶ЧКҪб№ы | »сАы | І»ЕвІ»Ч¬ | ҝчЛр |
ёЕВК |
|
|
|
ЧўЈә![]() Ј¬
Ј¬![]()
ЈЁ1Ј©ИфјЧЎўТТБҪИЛ·ЦұрСЎФсБЛІъЖ·![]() Н¶ЧКЈ¬Т»ДкәуЛыГЗЦРЦБЙЩУРТ»ИЛ»сАыөДёЕВКҙуУЪ
Н¶ЧКЈ¬Т»ДкәуЛыГЗЦРЦБЙЩУРТ»ИЛ»сАыөДёЕВКҙуУЪ![]() Ј¬ЗуКөКэ
Ј¬ЗуКөКэ![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
ЈЁ2Ј©ИфұыТӘҪ«20НтФӘИЛГсұТН¶ЧКЖдЦРТ»ЦЦІъЖ·Ј¬ТФТ»ДкәуөДН¶ЧККХТжөДЖЪНыЦөОӘҫцІЯТАҫЭЈ¬ФтұыСЎФсДДЦЦІъЖ·Н¶ЧКҪПОӘАнПл.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј®
Ј®
(1) Иф![]() Ј¬Зу
Ј¬Зу![]() өДЧоРЎЦөЈ»
өДЧоРЎЦөЈ»
(2) Иф![]() ФЪ
ФЪ![]() ЙПөҘөчөЭФцЈ¬Зу
ЙПөҘөчөЭФцЈ¬Зу![]() өДИЎЦө·¶О§Ј»
өДИЎЦө·¶О§Ј»
(3) Иф![]() Ј¬
Ј¬![]() ЗуЦӨЈә
ЗуЦӨЈә![]() Ј®
Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈёЯИэ4°аУР50ГыС§ЙъҪшРРБЛТ»іЎН¶АәІвКФЈ¬ЖдЦРДРЙъ30ИЛЈ¬Е®Йъ20ИЛЈ®ОӘБЛБЛҪвЖдН¶АәіЙјЁЈ¬јЧЎўТТБҪИЛ·Цұр¶ј¶ФИ«°аөДС§ЙъҪшРРұаәЕЈЁ1-50әЕЈ©Ј¬ІўТФІ»Н¬өД·Ҫ·ЁҪшРРКэҫЭійСщЈ¬ЖдЦРТ»ИЛУГөДКЗПөНіійСщЈ¬БнТ»ИЛУГөДКЗ·ЦІгійСщЈ®ИфҙЛҙОН¶АәІвКФөДіЙјЁҙуУЪ»төИУЪ80·ЦКУОӘУЕРгЈ¬РЎУЪ80·ЦКУОӘІ»УЕРгЈ¬ТФПВКЗјЧЎўТТБҪИЛ·ЦұрійИЎөДСщұҫКэҫЭЈә
јЧійИЎөДСщұҫКэҫЭ
ұаәЕ | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 | 47 |
РФұр | ДР | Е® | ДР | ДР | Е® | ДР | Е® | ДР | Е® | Е® |
Н¶АәіЙ јЁ | 90 | 60 | 75 | 80 | 83 | 85 | 75 | 80 | 70 | 60 |
ТТійИЎөДСщұҫКэҫЭ
ұаәЕ | 1 | 8 | 10 | 20 | 23 | 28 | 33 | 35 | 43 | 48 |
РФұр | ДР | ДР | ДР | ДР | ДР | ДР | Е® | Е® | Е® | Е® |
Н¶АәіЙ јЁ | 95 | 85 | 85 | 70 | 70 | 80 | 60 | 65 | 70 | 60 |
ЈЁўсЈ©ФЪТТійИЎөДСщұҫЦРИОИЎ3ИЛЈ¬јЗН¶АәУЕРгөДС§ЙъИЛКэОӘ![]() Ј¬Зу
Ј¬Зу![]() өД·ЦІјБРәНКэС§ЖЪНыЈ®
өД·ЦІјБРәНКэС§ЖЪНыЈ®
ЈЁўтЈ©ЗлДгёщҫЭТТійИЎөДСщұҫКэҫЭНкіЙПВБР2ЎБ2БРБӘұнЈ¬ЕР¶ПКЗ·сУР95%ТФЙПөД°СОХИПОӘН¶АәіЙјЁәНРФұрУР№ШЈҝ
УЕРг | ·ЗУЕРг | әПјЖ | |
ДР | |||
Е® | |||
әПјЖ | 10 |
ЈЁўуЈ©ЕР¶ПјЧЎўТТёчУГәОЦЦійСщ·Ҫ·ЁЈ¬ІўёщҫЭЈЁўтЈ©өДҪбВЫЕР¶ПДДЦЦійСщ·Ҫ·ЁёьУЕЈҝЛөГчАнУЙ.
ПВГжөДБЩҪзЦөұн№©ІОҝјЈә
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
ЈЁІОҝј№«КҪЈә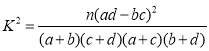 Ј¬ЖдЦР
Ј¬ЖдЦР![]() Ј©
Ј©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіН¬С§УГЎ°Лж»ъДЈДв·Ҫ·ЁЎұјЖЛгЗъПЯ![]() УлЦұПЯ
УлЦұПЯ![]() ЛщО§іЙөДЗъұЯИэҪЗРОөДГж»эКұЈ¬УГјЖЛг»ъ·ЦұрІъЙъБЛ10ёцФЪЗшјд[1Ј¬e]ЙПөДҫщФИЛж»ъКэxiәН10ёцФЪЗшјд[0Ј¬1]ЙПөДҫщФИЛж»ъКэ
ЛщО§іЙөДЗъұЯИэҪЗРОөДГж»эКұЈ¬УГјЖЛг»ъ·ЦұрІъЙъБЛ10ёцФЪЗшјд[1Ј¬e]ЙПөДҫщФИЛж»ъКэxiәН10ёцФЪЗшјд[0Ј¬1]ЙПөДҫщФИЛж»ъКэ![]()
![]() Ј¬ЖдКэҫЭИзПВұнөДЗ°БҪРРЈ®
Ј¬ЖдКэҫЭИзПВұнөДЗ°БҪРРЈ®
x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
lnx | 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
УЙҙЛҝЙөГХвёцЗъұЯИэҪЗРОГж»эөДТ»ёцҪьЛЖЦөОӘЈЁ Ј©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэБР![]() Ўў
Ўў![]() ВъЧг
ВъЧг![]() Ј¬ЗТ
Ј¬ЗТ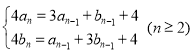
ЈЁ1Ј©Бо![]() ЦӨГчЈә
ЦӨГчЈә![]() КЗөИІоКэБРЈ¬
КЗөИІоКэБРЈ¬![]() КЗөИұИКэБРЈ»
КЗөИұИКэБРЈ»
ЈЁ2Ј©ЗуКэБР![]() әН
әН![]() өДНЁПКҪЈ»
өДНЁПКҪЈ»
ЈЁ3Ј©ЗуКэБР![]() әН
әН![]() өДЗ°nПоәН№«КҪЈ®
өДЗ°nПоәН№«КҪЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЛДАвЧ¶P-ABCDЦРЈ¬ЛДұЯРОABCDКЗЦұҪЗМЭРО,![]() өЧГж
өЧГж![]() ,
,![]() ,
,![]() ,
,![]() КЗ
КЗ![]() өДЦРөг.
өДЦРөг.
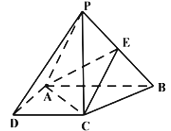
(1)ЗуЦӨЈәЖҪГж![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
(2)Иф![]() УлЖҪГж
УлЖҪГж![]() ЛщіЙҪЗөДХэПТЦөОӘ
ЛщіЙҪЗөДХэПТЦөОӘ![]() ,Зу¶юГжҪЗ
,Зу¶юГжҪЗ![]() өДУаПТЦө.
өДУаПТЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©ЈҪ|2x©Ғa|+|x©Ғ1|
ЈЁ1Ј©ИфfЈЁ1Ј©ЎЭ2Ј¬ЗуКөКэaөДИЎЦө·¶О§
ЈЁ2Ј©ИфІ»өИКҪfЈЁxЈ©ЎЬx¶ФИОТвx![]() [2Ј¬
[2Ј¬![]() ]әгіЙБўЈ¬ЗуКөКэaөДИЎЦө·¶О§Ј®
]әгіЙБўЈ¬ЗуКөКэaөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com