
分析 (1)设出直线AB的方程与抛物线方程联立,利用韦达定理求得y1y2,x1x2的值;
(2)分别表示出两个切线方程,联立可求得Q的坐标.表示出点Q到直线AB的距离,线段AB的长度,利用三角形面积公式表示出三角形面积,解方程即可得到m,进而得到直线AB的方程.
解答 (1)解:设直线AB的方程为x=my+1,
与抛物线方程联立得y2-my-1=0,
△=m2+4>0,
∴y1y2=-1,x1x2=y12y22=1;
(2)证明:由y2=x两边对x求导,可得2yy′=1,
即有y′=$\frac{1}{2y}$,
由导数的几何意义知在点(x0,y0)(y0≠0)处的切线斜率为$\frac{1}{2{y}_{0}}$;
∴切线QA的方程为y-y1=$\frac{1}{2{y}_{1}}$(x-y12),
即为x-2y1y+y12=0①
同理过B的切线方程为x-2y2y+y22=0②,
由①②,结合(1)的y1+y2=m,y1y2=-1,
可得x=-1,y=$\frac{m}{2}$,即有Q(-1,$\frac{m}{2}$),
∵x1+x2=4k,x1x2=-8,
∵点Q到直线AB:x=my+1的距离为d=$\frac{|-1-\frac{{m}^{2}}{2}-1|}{\sqrt{1+{m}^{2}}}$=$\frac{4+{m}^{2}}{2\sqrt{1+{m}^{2}}}$,
线段AB的长度为$\sqrt{1+{m}^{2}}$|y1-y2|=$\sqrt{1+{m}^{2}}$•$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{1+{m}^{2}}$•$\sqrt{4+{m}^{2}}$,
S=$\frac{1}{2}$•$\frac{4+{m}^{2}}{2\sqrt{1+{m}^{2}}}$•$\sqrt{1+{m}^{2}}$•$\sqrt{4+{m}^{2}}$=$\frac{5\sqrt{5}}{4}$,
解得m=±1,
即有直线AB的方程为x-y-1=0或x+y-1=0.
点评 本题主要考查了抛物线与直线的位置关系,点到直线距离公式的应用.考查了学生分析推理和运算的能力.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$与y=x | B. | y=x0与y=1 | ||
| C. | y=2${\;}^{lo{g}_{4}x}$与y=$\frac{x}{\sqrt{x}}$ | D. | y=x与y=($\sqrt{x})^{2}$2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
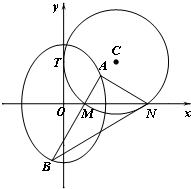 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(11,992).
把正整数数列的所有数按照从小到大的原则写成如图所示的数表,第k行有2k-1个数,第k行的第s个数(从左数起)记为A(k,s),则2015这个数可记为A(11,992).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1200 | B. | 1190 | C. | 1140 | D. | 95 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com