
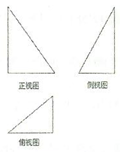
| A. | $\sqrt{6}π$ | B. | $\frac{4}{3}π$ | C. | 4π | D. | 6π |
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{\sqrt{3}}{3}$,0] | B. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | C. | [0,$\frac{\sqrt{3}}{3}$] | D. | (-∞,$\frac{\sqrt{3}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
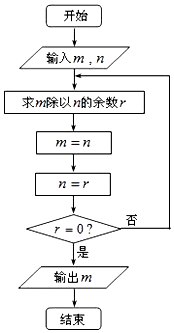 如图所示的程序框图描述的算法称为“欧几里得”辗转相除法,若输入m=2821,n=2015,则输出的m的值为( )
如图所示的程序框图描述的算法称为“欧几里得”辗转相除法,若输入m=2821,n=2015,则输出的m的值为( )| A. | 1 | B. | 403 | C. | 806 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
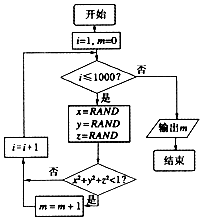 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为527,则由此可估计π的近似值为( )| A. | 3.126 | B. | 3.132 | C. | 3.151 | D. | 3.162 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com