
���� ��������ģ�����ʵó�|$\overrightarrow{a}$|�ķ�Χ������|$\overrightarrow{a}$|=2|$\overrightarrow{b}-\overrightarrow{a}$|�ó�$\overrightarrow{a}$��$\overrightarrow{b}$�Ĺ�ϵ��Ȼ�������������˵�ȡֵ��Χ��
��� ��|$\overrightarrow{a}$|=2|$\overrightarrow{b}-\overrightarrow{a}$|��
�࣬|$\overrightarrow{a}$|2=4��|$\overrightarrow{b}-\overrightarrow{a}$|��2��
��3|$\overrightarrow{a}$|2-8$\overrightarrow{a}$•$\overrightarrow{b}$+4|$\overrightarrow{b}$|2=0
�ࣨ3$\overrightarrow{a}$-2$\overrightarrow{b}$����$\overrightarrow{a}$-2$\overrightarrow{b}$��=0
��$\overrightarrow{a}$=$\frac{2}{3}$$\overrightarrow{b}$��$\overrightarrow{a}$=2$\overrightarrow{b}$
��1����$\overrightarrow{a}$=$\frac{2}{3}$$\overrightarrow{b}$ʱ��
��|$\overrightarrow{a}$+��$\overrightarrow{b}$|��3�������
��|$\frac{2}{3}$$\overrightarrow{b}$+��$\overrightarrow{b}$|��3�������
��|$\frac{2}{3}$+��|��1
��$\frac{2}{3}$+�ˡ�1��$\frac{2}{3}$+�ˡ�-1
��ˡ�$\frac{1}{3}$��ˡ�-$\frac{5}{3}$��
��2����$\overrightarrow{a}$=2$\overrightarrow{b}$ʱ
��|$\overrightarrow{a}$+��$\overrightarrow{b}$|��3�������
��|2$\overrightarrow{b}$+��$\overrightarrow{b}$|��3�����
��|��+2|��1
��ˡ�-1��ˡ�-3
��ʵ���˵�ȡֵ��ΧΪ��-�ޣ�-3]��[$\frac{1}{3}$��+�ޣ�
���������˵�ȡֵ��ΧΪ��-�ޣ�-3]��[$\frac{1}{3}$��+�ޣ���
���� ���⿼����ƽ�����������������㣬�����е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$-\frac{1}{2}$ | B�� | -1 | C�� | $\frac{1}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{e}f��2����f��1��$ | B�� | $\frac{2}{e}f��2����f��1��$ | C�� | f��1����0 | D�� | f��-1����0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | 2 | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
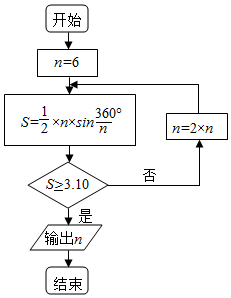 �ҹ�κ���ڼ��ΰ�����ѧ�����գ�������������������ķ�ʽ����֤��ѧ������ˣ��������ˡ���Բ�������õ��������ġ����ʡ�����Բ���ʾ�ȷ��С�������λ�Ľ���ֵ3.14����ͼ�������á���Բ������˼����Ƶ�һ�������ͼ�����������n��ֵΪ���ο����ݣ�sin15��=0.2588��sin7.5��=0.1305����������
�ҹ�κ���ڼ��ΰ�����ѧ�����գ�������������������ķ�ʽ����֤��ѧ������ˣ��������ˡ���Բ�������õ��������ġ����ʡ�����Բ���ʾ�ȷ��С�������λ�Ľ���ֵ3.14����ͼ�������á���Բ������˼����Ƶ�һ�������ͼ�����������n��ֵΪ���ο����ݣ�sin15��=0.2588��sin7.5��=0.1305����������| A�� | 12 | B�� | 24 | C�� | 36 | D�� | 48 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{6}��$ | B�� | $\frac{4}{3}��$ | C�� | 4�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com