练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．求证：$\underset{lim}{x→0}$$\frac{{e}^{\frac{1}{x}+1}}{{e}^{\frac{1}{x}}-1}$不存在．

    分析 化简$\underset{lim}{x→{0}^{-}}$$\frac{{e}^{\frac{1}{x}+1}}{{e}^{\frac{1}{x}}-1}$=$\frac{1}{-1}$=-1，$\underset{lim}{x→{0}^{+}}$$\frac{{e}^{\frac{1}{x}+1}}{{e}^{\frac{1}{x}}-1}$=$\underset{lim}{x→{0}^{+}}$$\frac{1+\frac{1}{{e}^{\frac{1}{x}}}}{1-\frac{1}{{e}^{\frac{1}{x}}}}$=1，从而证明．

    解答 证明：∵$\underset{lim}{x→{0}^{-}}$$\frac{{e}^{\frac{1}{x}+1}}{{e}^{\frac{1}{x}}-1}$=$\frac{1}{-1}$=-1，$\underset{lim}{x→{0}^{+}}$$\frac{{e}^{\frac{1}{x}+1}}{{e}^{\frac{1}{x}}-1}$=$\underset{lim}{x→{0}^{+}}$$\frac{1+\frac{1}{{e}^{\frac{1}{x}}}}{1-\frac{1}{{e}^{\frac{1}{x}}}}$=1，
    ∴$\underset{lim}{x→0}$$\frac{{e}^{\frac{1}{x}+1}}{{e}^{\frac{1}{x}}-1}$不存在．

    点评 本题考查了极限的求法与应用及分类讨论的思想应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=2sin（ωx）cos（ωx）+msin2（ωx）（ω＞0）关于点（$\frac{π}{12}，1$）对称
    （Ⅰ）求m的值及f（x）的最小值；
    （Ⅱ）在△ABC中，角A，B，C所对应的边分别为a，b，c，最大内角A的值为f（x）的最小正周期，若b=2，△ABC面积的取值范围为[$\frac{\sqrt{3}}{2}，\sqrt{3}$]，求角A的值及a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=lnx-kx+1．
    （1）求函数f（x）的单调区间；
    （2）若f（x）≤0恒成立，试确定实数k的取值范围；
    （3）证明：ln[2•3•4•…（n+1）]2≤n（n+1）（n∈N，n＞1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知向量$\overrightarrow{OA}$=（λcosα，λsinα）（λ≠0），$\overrightarrow{OB}$=（-sinβ，cosβ），其中O为坐标原点．
    （1）若λ=1且α=$\frac{π}{2}$，β=$\frac{π}{3}$，求向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角；
    （2）若α-β=$\frac{π}{2}$，求使得|${\overrightarrow{BA}}$|≥2|${\overrightarrow{OB}}$|成立的λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

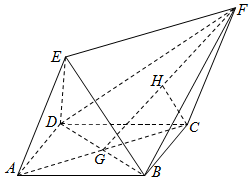    6．四边形ABCD为菱形，ACFE为平行四边形，且平面ACFE⊥平面ABCD，设BD与AC相交于点G，H为FG的中点，AB=BD=2，AE=$\sqrt{3}$，CH=$\frac{{\sqrt{3}}}{2}$．
    （Ⅰ）求证：CH⊥平面BDF；
    （Ⅱ）若Q为△DEF的重心，求QH与平面BEF所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．设函数f（x）=lnx+$\frac{a}{x}$（a∈R）．
    （Ⅰ）当a=1时，求函数f（x）的极小值；
    （Ⅱ）f（x）的导函数是f′（x），讨论函数g（x）=f′（x）-x的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．“所有金属都能导电，铁是金属，所以铁能导电．”这种推理属于（　　）
    A．类比推理B．合情推理C．归纳推理D．演绎推理

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．如表为甲、乙两位同学在最近五次模拟考试中的数学成绩（单位：分）
    甲102126131118127
    乙96117120119135
    （1）试判断甲、乙两位同学哪位同学的数学考试成绩更稳定？（不用计算，给出结论即可）
    （2）若从甲、乙两位同学的数学考试成绩中各随机抽取1次成绩进行分析，设抽到的成绩中130分以上的次数恰好为1次的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．若多项式（x+1）3+（x-1）8=a0+a1x+a2x2+…+a8x8．
    （1）求a2的值：
    （2）求a1-a2+a3-a4+a5-a6+a7-a8的值．

    查看答案和解析>>

    同步练习册答案