
已知数列{an}的相邻两项an,an+1是关于x的方程x2-2nx+bn=0的两根,且a1=1.
(1)求证:数列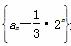 是等比数列;
是等比数列;
(2)求数列{an}的前n项和Sn;
(3)设函数f(n)=bn-t·Sn(n∈N*),若f(n)>0对任意的n∈N*都成立,求实数t的取值范围.
(1)∵ an+an+1=2n,
∴ an+1-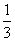 ·2n+1=-
·2n+1=-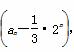 ,
,
∵ a1-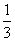 ·2=
·2=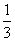 ≠0,
≠0,
∴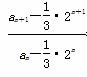 =-1,
=-1,
∴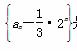 是首项为
是首项为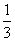 ,公比为-1的等比数列,
,公比为-1的等比数列,
且an=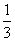 [2n-(-1)n].
[2n-(-1)n].
(2)由(1),得Sn=a1+a2+…+an=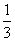 (2+22+…+2n)-
(2+22+…+2n)-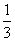 [(-1)+(-1)2+…+(-1)n]
[(-1)+(-1)2+…+(-1)n]
=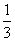
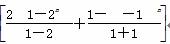
=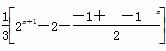
=
(3)∵ bn=an·an+1,
∴ bn= [2n-(-1)n][2n+1-(-1)n+1]=
[2n-(-1)n][2n+1-(-1)n+1]= [22n+1-(-2)n-1],
[22n+1-(-2)n-1],
∵ bn-t·Sn>0,
∴  [22n+1-(-2)n-1]-t·
[22n+1-(-2)n-1]-t·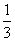
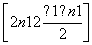 >0.
>0.
∴ 当n为奇数时,
 (22n+1+2n-1)-
(22n+1+2n-1)-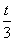 (2n+1-1)>0,
(2n+1-1)>0,
∵ t<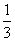 (2n+1)对任意的n为奇数都成立,∴ t<1.
(2n+1)对任意的n为奇数都成立,∴ t<1.
∴ 当n为偶数时,
 (22n+1-2n-1)-
(22n+1-2n-1)-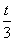 (2n+1-2)>0,
(2n+1-2)>0,
∴  (22n+1-2n-1)-
(22n+1-2n-1)-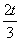 (2n-1)>0,
(2n-1)>0,
∵ t<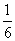 (2n+1+1)对任意的n为偶数都成立,∴ t<
(2n+1+1)对任意的n为偶数都成立,∴ t<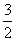 .
.
综上所述,实数t的取值范围为(-∞,1).


科目:高中数学 来源: 题型:
在数列{an}中,若对任意的n均有an+an+1+an+2为定值(n∈N*),且a7=2,a9=3,a98=4,则数列{an}的前100项的和S100等于( )
A.132 B.299
C.68 D.99
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=sin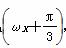 (x∈R,ω>0)的部分图象如图所示,点P是图象的最高点,Q是图象的最低点,且|PQ|=
(x∈R,ω>0)的部分图象如图所示,点P是图象的最高点,Q是图象的最低点,且|PQ|=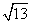 ,则f(x)的最小正周期是( )
,则f(x)的最小正周期是( )
A.6π B.4π C.4 D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2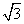 sin xcos x+2cos2x-1(x∈R).
sin xcos x+2cos2x-1(x∈R).
(1)求函数f(x)的最小正周期及在区间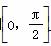 上的最大值和最小值;
上的最大值和最小值;
(2)若f(x0)=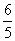 ,x0∈
,x0∈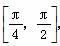 ,求cos 2x0的值.
,求cos 2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设两向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com