练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)的图象与函数h(x)＝x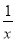＋＋2的图象关于点A(0,1)对称．

    (1)求函数f(x)的解析式；

    (2)若g(x)＝f(x)＋，g(x)在区间(0,2]上的值不小于6，求实数a的取值范围．

     

    （1）f(x)＝x＋

    （2）[7，＋∞)

    【解析】【解析】
    (1)设f(x)图象上任一点坐标为(x，y)，∵点(x，y)关于点A(0,1)的对称点(－x,2－y)在h(x)的图象上，

    ∴2－y＝－x＋＋2，∴y＝x＋，即f(x)＝x＋.

    (2)由题意g(x)＝x＋，且g(x)＝x＋≥6，x∈(0,2]．

    ∵x∈(0,2]，∴a＋1≥x(6－x)，

    即a≥－x2＋6x－1.令q(x)＝－x2＋6x－1，x∈(0,2]，

    q(x)＝－x2＋6x－1＝－(x－3)2＋8，∴x∈(0,2]时，

    q(x)max＝q(2)＝7，

    故a的取值范围为[7，＋∞)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-9函数模型及其应用（解析版） 题型：填空题

    某厂去年的产值为1，若计划在今后五年内每年的产值比上年增长10%，则从今年起到第五年这五年内，这个厂的总产值约为________．(保留一位小数，取1.15≈1.6)

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-6对数与对数函数（解析版） 题型：选择题

    设a＝lg e，b＝(lg e)2，c＝lg，则(　　)

    A．a>b>c B．a>c>b

    C．c>a>b D．c>b>a

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-5指数及指数函数（解析版） 题型：填空题

    已知函数f(x)＝|2x－1|，a<b<c，且f(a)>f(c)>f(b)，则下列结论中，一定成立的是________．

    ①a<0，b<0，c<0; ②a<0，b≥0，c>0；③2－a<2c; ④2a＋2c<2.

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-5指数及指数函数（解析版） 题型：选择题

    已知f(x)＝2x＋2－x，若f(a)＝3，则f(2a)等于(　　)

    A．5 B．7 C．9 D．11

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：填空题

    已知f(x)＝ax2＋bx＋3a＋b是偶函数，且其定义域为[a－1,2a]，则y＝f(x)的值域为______．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-3函数的奇偶性与周期性（解析版） 题型：解答题

    已知函数f(x)对任意实数x，y恒有f(x＋y)＝f(x)＋f(y)，且当x>0时，f(x)<0，又f(1)＝－2.

    (1)判断f(x)的奇偶性；

    (2)求证：f(x)是R上的减函数；

    (3)求f(x)在区间[－3,3]上的值域；

    (4)若?x∈R，不等式f(ax2)－2f(x)<f(x)＋4恒成立，求a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-2函数的单调性与最值（解析版） 题型：填空题

    设函数f(x)＝ (x＋|x|)，则函数f[f(x)]的值域为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-12导数的应用二（解析版） 题型：选择题

    若函数f(x)＝x3－3x在(a,6－a2)上有最小值，则实数a的取值范围是(　　)

    A．(－，1) B．[－，1)

    C．[－2,1) D．(－2,1)

     

    查看答案和解析>>

    同步练习册答案