已知f(x)＝ax2＋bx＋3a＋b是偶函数，且其定义域为[a－1,2a]，则y＝f(x)的值域为______．
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-9函数模型及其应用（解析版） 题型：选择题
台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，B城市处于危险区内的时间为( )
A．0.5小时 B．1小时 C．1.5小时 D．2小时
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-6对数与对数函数（解析版） 题型：填空题
如果函数y＝f(x)图象上任意一点的坐标(x，y)都满足方程lg(x＋y)＝lgx＋lgy，那么y＝f(x)在[2,4]上的最小值是________．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-5指数及指数函数（解析版） 题型：选择题
函数y＝(
)
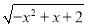的单调递增区间是( )
A．[－1，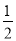
] B．(－∞，－1]
C．[2，＋∞) D．[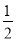
，2]
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：解答题
已知函数f(x)的图象与函数h(x)＝x＋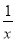
＋2的图象关于点A(0,1)对称．
(1)求函数f(x)的解析式；
(2)若g(x)＝f(x)＋
，g(x)在区间(0,2]上的值不小于6，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：选择题
图中曲线是幂函数y＝xn在第一象限的图象，已知n取±2，±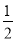
四个值，则对应于曲线C1，C2，C3，C4的n值依次为( )
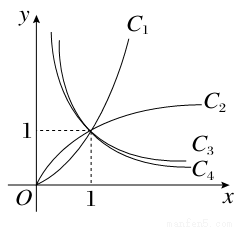
A．－2，－
，
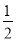，2 B．2，
，－
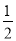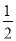，－2
C．－
，－2,2，
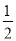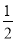D．2，
，－2，－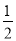
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-3函数的奇偶性与周期性（解析版） 题型：解答题
已知f(x)是偶函数，且f(x)在[0，＋∞)上是增函数，如果f(ax＋1)≤f(x－2)在x∈[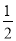
，1]上恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-2函数的单调性与最值（解析版） 题型：填空题
设函数f(x)的图象关于y轴对称，又已知f(x)在(0，＋∞)上为减函数，且f(1)＝0，则不等式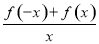
<0的解集为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
]
，
x2＋1，x∈[－
，
]，其值域为{y|1≤y≤
}．
