
【题目】已知函数![]() .
.
(1)若函数![]() 有一个极小值点和一个极大值点,求
有一个极小值点和一个极大值点,求![]() 的取值范围;
的取值范围;
(2)设![]() ,若存在
,若存在![]() ,使得当
,使得当![]() 时,
时, ![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)求出函数![]() 的导数,由函数
的导数,由函数![]() 有两个极值点,得到关于
有两个极值点,得到关于![]() 的不等式组,求得实数
的不等式组,求得实数![]() ,再作出验算即可.
,再作出验算即可.
(2)求出![]() 的导数,通过讨论
的导数,通过讨论![]() 的范围确定函数的单调区间,得到关于
的范围确定函数的单调区间,得到关于![]() 的不等式,解出即可.
的不等式,解出即可.
试题解析:
(1) ![]() ,则
,则![]()
令![]() ,若函数
,若函数![]() 有两个极值点,则方程
有两个极值点,则方程![]() 必有两个不等的正根,于是
必有两个不等的正根,于是 解得
解得![]()
当![]() 时,
时, ![]() 有两个不相等的正实根,设为
有两个不相等的正实根,设为![]() ,不妨设
,不妨设![]() ,
,
则![]() .
.
当![]() 时,
时, ![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时, ![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时, ![]() 函数
函数![]() 在
在![]() 上为减函数.
上为减函数.
由此, ![]() 是函数
是函数![]() 的极小值点,
的极小值点, ![]() 是函数
是函数![]() 的极大值点.符合题意.
的极大值点.符合题意.
综上,所求实数![]() 的取值范围是
的取值范围是![]()
(2)![]()
①当![]() 时,
时, ![]() .当
.当![]() 时,
时, ![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时, ![]() 在
在![]() 上为增函数.
上为增函数.
所以,当![]() 时,
时, ![]() 的值域是
的值域是![]() .
.
不符合题意.
当![]() 时,
时, 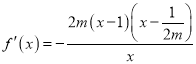 .
.
(i)当![]() ,即
,即![]() 时,
时, ![]() , 当且仅当
, 当且仅当![]() 时取等号.
时取等号.
所以![]() 在
在![]() 上为减函数.从而
上为减函数.从而![]() 在
在![]() 上为减函数.符合题意
上为减函数.符合题意
(ii)当![]() ,即
,即![]() 时,当
时,当![]() 变化时,
变化时, ![]() 的变化情况如下表:
的变化情况如下表:
|
| 1 |
|
|
|
| - | 0 | + | 0 | - |
| 减函数 | 极小值0 | 增函数 | 极大值 | 减函数 |
若满足题意,只需满足![]() ,且
,且![]() (若
(若![]() ,不符合题意),即
,不符合题意),即![]() ,
,
且![]() .又
.又![]() ,所以
,所以![]() ,此时
,此时![]()
所以实数![]() 的取值范围是
的取值范围是![]()


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】为了调查学生数学学习的质量情况,某校从高二年级学生(其中男生与女生的人数之比为![]() )中,采用分层抽样的方法抽取
)中,采用分层抽样的方法抽取![]() 名学生依期中考试的数学成绩进行统计.根据数学的分数取得了这
名学生依期中考试的数学成绩进行统计.根据数学的分数取得了这![]() 名同学的数据,按照以下区间分为八组:
名同学的数据,按照以下区间分为八组:
①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,⑥
,⑥![]() ,⑦
,⑦![]() ,⑧
,⑧![]()
得到频率分布直方图如图所示.已知抽取的学生中数学成绩少于![]() 分的人数为
分的人数为![]() 人.
人.

(1)求![]() 的值及频率分布直方图中第④组矩形条的高度;
的值及频率分布直方图中第④组矩形条的高度;
(2)如果把“学生数学成绩不低于![]() 分”作为是否达标的标准,对抽取的
分”作为是否达标的标准,对抽取的![]() 名学生,完成下列
名学生,完成下列![]() 列联表:
列联表:

据此资料,你是否认为“学生性别”与“数学成绩达标与否”有关?
(3)若从该校的高二年级学生中随机抽取![]() 人,记这
人,记这![]() 人中成绩不低于
人中成绩不低于![]() 分的学生人数为
分的学生人数为![]() ,求
,求![]() 的分布列、数学期望和方差
的分布列、数学期望和方差
附1:“![]() 列联表
列联表![]() ”的卡方统计量公式:
”的卡方统计量公式:![]()
附2:卡方(![]() )统计量的概率分布表:
)统计量的概率分布表:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与曲线
与曲线![]() 恰有两个不同的交点,记
恰有两个不同的交点,记![]() 的所有可能取值构成集合
的所有可能取值构成集合![]() ,
,![]() 是椭圆
是椭圆![]() 上一动点,点
上一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,记
对称,记![]() 的所有可能取值构成集合
的所有可能取值构成集合![]() ,若随机从集合
,若随机从集合![]() 中分别抽出一个元素
中分别抽出一个元素![]() ,则
,则![]() 的概率是___.
的概率是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面α及直线a,b,则下列说法正确的是( )
A. 若直线a,b与平面α所成角都是30°,则这两条直线平行
B. 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直
C. 若直线a,b平行,则这两条直线中至少有一条与平面α平行
D. 若直线a,b垂直,则这两条直线与平面α不可能都垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com