
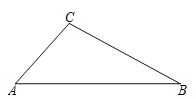
【题目】如图,已知![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 面积的最大值;
面积的最大值;
(Ⅱ)若![]() ,求
,求![]() .
.
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,PA=2,∠ABC=90°,![]() ,BC=1,
,BC=1, ![]() ,∠ACD=60°,E为CD的中点.
,∠ACD=60°,E为CD的中点.

(1)求证:BC∥平面PAE;
(2)求点A到平面PCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题α:函数![]() 的定义域是R;命题β:在R上定义运算:xy=x(1-y).不等式(x-a)(x+a)<1对任意实数x都成立.
的定义域是R;命题β:在R上定义运算:xy=x(1-y).不等式(x-a)(x+a)<1对任意实数x都成立.
(1)若α、β中有且只有一个真命题,求实数a的取值范围;
(2)若α、β中至少有一个真命题,求实数a的取值范围;
(3)若α、β中至多有一个真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个人下半身长(肚脐至足底)与全身长的比近似为![]() (
(![]() ,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72
,称为黄金分割比),堪称“身材完美”,且比值越接近黄金分割比,身材看起来越好,若某人着装前测得头顶至肚脐长度为72![]() ,肚脐至足底长度为103
,肚脐至足底长度为103![]() ,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
,根据以上数据,作为形象设计师的你,对TA的着装建议是( )
A.身材完美,无需改善B.可以戴一顶合适高度的帽子
C.可以穿一双合适高度的增高鞋D.同时穿戴同样高度的增高鞋与帽子
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 是等边三角形且垂直于底面
是等边三角形且垂直于底面![]() ,底面
,底面![]() 是矩形,
是矩形,![]() ,
,![]() 是
是![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与直线
与直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com