
分析 (Ⅰ)先求导,根据导数和函数的最值的关系即可求出k的值,
(Ⅱ)由题意转化为(1-$\frac{{x}_{1}}{{x}_{2}}$)+$\frac{1}{2}$($\frac{{x}_{1}}{{x}_{2}}$+1)ln$\frac{{x}_{1}}{{x}_{2}}$<0,构造函数g(t)=(1-t)+$\frac{1}{2}$(t+1)lnt,利用函数的导数和函数的最值的关系即可证明.
解答 解:(Ⅰ)f′(x)=$\frac{1-lnkx}{{x}^{2}}$,当0<k≤$\frac{1}{\sqrt{e}}$时,f(x)max=f(${e}^{\frac{3}{2}}$)=$\frac{1}{e}$⇒k=${e}^{\sqrt{e}-\frac{3}{2}}$>$\frac{1}{\sqrt{e}}$,舍去;
当k>$\frac{1}{\sqrt{e}}$时,f(x)max=f($\frac{e}{k}$)=$\frac{1}{e}$⇒k=1,
∴k=1.
(Ⅱ)∵f(x)=$\frac{lnx}{x}$,
∴f′(x)=$\frac{1-lnx}{{x}^{2}}$,令m(x)=f′(x),
∴m′(x)=$\frac{-3+2lnx}{{x}^{3}}$<0,
∴f′(x)在(0,${e}^{\frac{3}{2}}$)上递减,要证x0<$\sqrt{{x}_{1}{x}_{2}}$,只需证明f′(x0)>f′($\sqrt{{x}_{1}{x}_{2}}$),
而f′($\sqrt{{x}_{1}{x}_{2}}$)-f′(x0)=$\frac{1-ln\sqrt{{x}_{1}{x}_{2}}}{{x}_{1}{x}_{2}}$-$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$=$\frac{\frac{ln{x}_{2}}{{x}_{2}}-\frac{ln{x}_{1}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$=$\frac{1}{{x}_{1}{x}_{2}}$[1-ln$\sqrt{{x}_{1}{x}_{2}}$-$\frac{{x}_{1}ln{x}_{2}-{x}_{2}ln{x}_{1}}{{x}_{2}-{x}_{1}}$],
∴x1,x2∈(0,e${\;}^{\frac{3}{2}}$],x1-x2<0,
只需证明(x2-x1)[1-ln$\sqrt{{x}_{1}{x}_{2}}$]-(x1lnx2-x2lnx1)<0,
也就是证明(x2-x1)+$\frac{1}{2}$(x2+x1)ln$\frac{{x}_{1}}{{x}_{2}}$<0,
即证(1-$\frac{{x}_{1}}{{x}_{2}}$)+$\frac{1}{2}$($\frac{{x}_{1}}{{x}_{2}}$+1)ln$\frac{{x}_{1}}{{x}_{2}}$<0,
令$\frac{{x}_{1}}{{x}_{2}}$=t,t∈(0,1),即是要证明t∈(0,1)时,(1-t)+$\frac{1}{2}$(t+1)lnt<0恒成立,
令g(t)=(1-t)+$\frac{1}{2}$(t+1)lnt,g(1)=0,
∴g′(t)=$\frac{tlnt-t-1}{t}$,g′(1)=0,.
设k(t)=t-tlnt-1,
∴k′(t)=-lnt<0(t>1),
∴k(t)在(1,+∞)是减函数,
∴k(t)<k(1)=0.
∴g′(t)<0,
∴g(t)在(1,+∞)是减函数,
∴g(t)<g(1)=0,
∴x0<$\sqrt{{x}_{1}{x}_{2}}$.
点评 本题考查了导数在最值中的应用,考查了利用导数研究函数的单调性,考查了换元法和数学转化思想,解答此题的关键是两次构造辅助函数,是较难的题目.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
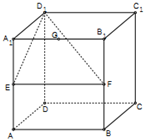 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若p,则q”与命题“若非q,则非p”互为逆否命题 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若f′(x)=0,则x为y=f(x)的极值点”为真命题 | |
| D. | “am2<bm2”是“a<b”的充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com