
分析 (Ⅰ)由平面向量数量积的运算可得$\overrightarrow a•\overrightarrow b$=2cos2x-1,|$\overrightarrow a+\overrightarrow b$|=2|cosx|,结合x的范围,即可得解.
(Ⅱ)由(Ⅰ)可得f(x)=2(cosx+1)2-3,结合x的范围即可求得最小值.
解答 解:(Ⅰ)$\overrightarrow a•\overrightarrow b$=$cos\frac{3x}{2}$$cos\frac{x}{2}$-$sin\frac{3x}{2}$$sin\frac{x}{2}$=cos2x=2cos2x-1,----(2分)
|$\overrightarrow a+\overrightarrow b$|=$\sqrt{{{({cos\frac{3x}{2}+cos\frac{x}{2}})}^2}+{{({sin\frac{3x}{2}-sin\frac{x}{2}})}^2}}$=$\sqrt{2+2cos2x}$=2|cosx|,
∵$x∈[0,\frac{π}{2}]$,∴cosx≥0,
∴|$\overrightarrow a+\overrightarrow b$|=2cosx.-----(5分)
(Ⅱ)f(x)=$\overrightarrow a•\overrightarrow b$+2|$\overrightarrow a+\overrightarrow b$|=2cos2x-1+4cosx=2(cosx+1)2-3,-------(7分)
∵$x∈[0,\frac{π}{2}]$,
∴0≤cosx≤1,
∴当cosx=0时,f(x)取得最小值-1.-------(10分)
点评 本题主要考查了平面向量数量积的运算,两角和与差的正弦函数公式的应用,余弦函数的图象和性质,属于基本知识的考查.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
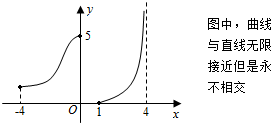
| A. | 函数f(x)的定义域为[-4,4) | |
| B. | 函数f(x)的值域为[0,5] | |
| C. | 此函数在定义域内既不是增函数也不是减函数 | |
| D. | 对于任意的y∈[0,+∞),都有唯一的自变量x与之对应 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由样本数据得到的回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过样本中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好 | |
| D. | 两个随机变量的线性相关性越强,相关系数的绝对值越接近于1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±2 | C. | 4 | D. | ±4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)=2sin(ωx+θ ) (ω>0)的图象如图所示,则ω=2,若将函数f(x)的图象向左平移φ $({0<φ<\frac{π}{2}})$个单位后得到一个偶函数,则φ=$\frac{π}{3}$.
已知函数f(x)=2sin(ωx+θ ) (ω>0)的图象如图所示,则ω=2,若将函数f(x)的图象向左平移φ $({0<φ<\frac{π}{2}})$个单位后得到一个偶函数,则φ=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,F在AD上且∠FCD=30°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,F在AD上且∠FCD=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com