
| A. | a≤15 | B. | 0<a≤15 | C. | a>6 | D. | a<-3 |
分析 首先,不等式$\frac{f(p+1)-f(q+1)}{p-q}$<1恒成立,即为$\frac{f(p+1)-p-[f(q+1)-q]}{p-q}$<0,构造函数g(x)=f(x+1)-x在(1,2)递减,分离参数后,得到a≤2x2+7x+6在(1,2)内恒成立.从而求解得到a的取值范围.
解答 解:∵$\frac{f(p+1)-f(q+1)}{p-q}$的几何意义为:
表示点(p+1,f(p+1)) 与点(q+1,f(q+1))连线的斜率,
∵实数p,q在区间(1,2)内,故p+1 和q+1在区间(2,3)内.
不等式$\frac{f(p+1)-f(q+1)}{p-q}$<1恒成立,即为$\frac{f(p+1)-p-[f(q+1)-q]}{p-q}$<0,
∴构造函数g(x)=f(x+1)-x在(1,2)递减,
故函数的导数小于等于0在(1,2)内恒成立.
由函数的定义域知,x>-2,
∴g′(x)=$\frac{a}{x+2}$-2(x+1)-1≤0 在(1,2)内恒成立.
即a≤2x2+7x+6在(1,2)内恒成立.
由于二次函数y=2x2+7x+6在[1,2]上是单调增函数,
故x=1时,y=2x2+7x+6在[1,2]上取最小值为15,
∴a≤15.
故选:A.
点评 本题重点考查导数的应用,函数的几何性质等知识,注意分离参数在求解中的灵活运用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
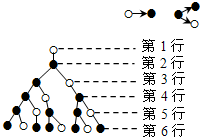 分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照
分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{9}{10}$,$\sqrt{2}$)∪(-1,-$\frac{9}{10}$) | B. | (-1,$\sqrt{2}$] | C. | (-1,-$\frac{9}{10}$) | D. | (-$\frac{9}{10}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有且只有一个 | B. | 有四个 | C. | 有无数个 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com