
分析 (1)作出不等式组表示的平面区域;作出目标函数对应的直线;结合图象知当直线过B(5,3)时,z最大,当直线过C时,z最小.
(2)作出不等式组$\left\{{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{y≥a(x-3)}\end{array}}\right.$.表示的平面区域,从而解出.
解答 解:(1)画出不等式$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{y≥2x-6}\end{array}\right.$表示的平面区域: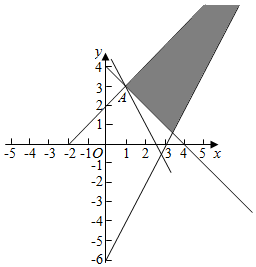
将目标函数变形为z=2x+y,作出目标函数对应的直线,$\left\{\begin{array}{l}{x+y-4=0}\\{x-y+2=0}\end{array}\right.$,解得A(1,3),
直线过A(1,3)时,直线的纵截距最大,z最小,最小值为5;
则目标函数z=2x+y的最小值为:5.
故答案为:5.
(2)$\left\{{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{y≥a(x-3)}\end{array}}\right.$.
如下图:
y=a(x-3)恒过(3,0),则若不等式组
表示的平面区域是一个三角形,KAB=$\frac{3-0}{1-3}$=-$\frac{3}{2}$,则实数a的取值范围,1<a或a<$-\frac{3}{2}$,
故答案为:1<a或a<$-\frac{3}{2}$.
点评 本题考查画不等式组表示的平面区域、考查数形结合求函数的最值.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | ||
| 第二组 | (25,50] | ||
| 第三组 | (50,75] | ||
| 第四组 | (75,100] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,它的部分图象如图所示.M是函数f(x)图象上的点,K,L是函数f(x)的图象与x轴的交点,且△KLM为等腰直角三角形,则f(x)=$\frac{1}{2}$cosπx.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,它的部分图象如图所示.M是函数f(x)图象上的点,K,L是函数f(x)的图象与x轴的交点,且△KLM为等腰直角三角形,则f(x)=$\frac{1}{2}$cosπx.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
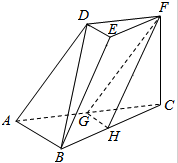 如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com