
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,它的部分图象如图所示.M是函数f(x)图象上的点,K,L是函数f(x)的图象与x轴的交点,且△KLM为等腰直角三角形,则f(x)=$\frac{1}{2}$cosπx.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,它的部分图象如图所示.M是函数f(x)图象上的点,K,L是函数f(x)的图象与x轴的交点,且△KLM为等腰直角三角形,则f(x)=$\frac{1}{2}$cosπx. 分析 由函数的最值求出A,由函数的奇偶性求出φ的值,由周期求出ω,可得函数的解析式.
解答 解:由题意可得A=$\frac{1}{2}$,φ=2kπ+$\frac{π}{2}$,k∈Z,再结合0<φ<π,可得φ=$\frac{π}{2}$,
函数f(x)=$\frac{1}{2}$sin(ωx+$\frac{π}{2}$)=$\frac{1}{2}$cosωx.
再根据$\frac{1}{4}$•$\frac{2π}{ω}$=$\frac{1}{2}$,可得ω=π,函数f(x)=$\frac{1}{2}$cosπx,
故答案为:$\frac{1}{2}$cosπx.
点评 由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由函数的奇偶性求出φ的值,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 23 | C. | 22 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
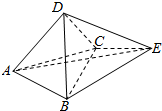 如图,正三棱锥A-BCD的底面与正四面体E-BCD的侧面BCD重合,连接AE,则异面直线AE与CD所成角的大小为( )
如图,正三棱锥A-BCD的底面与正四面体E-BCD的侧面BCD重合,连接AE,则异面直线AE与CD所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?m∈[0,1],则$x+\frac{1}{x}<{2^m}$ | B. | ?m∈[0,1],则$x+\frac{1}{x}≥{2^m}$ | ||
| C. | ?m∈(-∞,0)∪(1,+∞),则$x+\frac{1}{x}≥{2^m}$ | D. | ?m∈[0,1],则$x+\frac{1}{x}<{2^m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com