
已知函数 (
( 为常数)的图象与
为常数)的图象与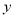 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为
处的切线斜率为 .
.
(Ⅰ)求 的值及函数
的值及函数 的极值;
的极值;
(Ⅱ)证明:当 时,
时, ;
;
(Ⅲ)证明:对任意给定的正数 ,总存在
,总存在 ,使得当
,使得当 ,恒有
,恒有 .
.
(Ⅰ) ,极小值为
,极小值为
 无极大值;(Ⅱ)详见解析;
无极大值;(Ⅱ)详见解析;
(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)由 ,得
,得 .再根据曲线
.再根据曲线 在点
在点 处的切线斜率为
处的切线斜率为 ,便可得
,便可得 从而得
从而得 .代入解析式得
.代入解析式得 .由此根据导数的符号即可得函数的极值;(Ⅱ)令
.由此根据导数的符号即可得函数的极值;(Ⅱ)令 .为了证
.为了证 ,只需证
,只需证 ,而这利用导数很易证明;
,而这利用导数很易证明;
(Ⅲ)由(Ⅱ)知,当 时,
时,  .所以当
.所以当 时必有
时必有 时,
时,  .取
.取 即可.若
即可.若 ,为了使问题简化,作以下转化:令
,为了使问题简化,作以下转化:令 ,要使不等式
,要使不等式 成立,只要
成立,只要 成立.而要使
成立.而要使 成立,则只要
成立,则只要 ,即
,即 成立.令
成立.令 ,这样转化后,这个函数的导数就很简单了,利用导数可找到
,这样转化后,这个函数的导数就很简单了,利用导数可找到 ,使得当
,使得当 ,恒有
,恒有 .
.
试题解析:解:(Ⅰ)由 ,得
,得 .
.
又 ,得
,得 .
.
所以 .
.
令 ,得
,得 .当
.当 时,
时,  单调递减;当
单调递减;当 时,
时,  单调递增. 所以当
单调递增. 所以当 时,
时,  取得极小值,且极小值为
取得极小值,且极小值为
 无极大值.
无极大值.
(Ⅱ)令 ,则
,则 .
.
由(Ⅰ)得 ,
,
故 在R上单调递增,又
在R上单调递增,又 ,
,
因此,当 时,
时,  ,即
,即 .
.
(Ⅲ)①若 ,则
,则 .又由(Ⅱ)知,当
.又由(Ⅱ)知,当 时,
时,  .
.
所以当 时,
时,  .取
.取 ,当
,当 时,恒有
时,恒有 .
.
②若 ,令
,令 ,要使不等式
,要使不等式 成立,只要
成立,只要 成立.而要使
成立.而要使 成立,则只要
成立,则只要 ,只要
,只要 成立.
成立.
令 ,则
,则 .
.
所以当 时,
时,  在
在 内单调递增.
内单调递增.
取 ,所以
,所以 在
在 内单调递增.
内单调递增.
又 .
.
易知 .所以
.所以 .即存在
.即存在 ,当
,当 时,恒有
时,恒有 .
.
综上,对任意给定的正数c,总存在 ,当
,当 时,恒有
时,恒有 . .....14分
. .....14分
解法二:(Ⅰ)同解法一(Ⅱ)同解法一(Ⅲ)对任意给定的正数c,取
由(Ⅱ)知,当x>0时, ,所以
,所以 ,当
,当 时,
时, 
因此,对任意给定的正数 ,总存在
,总存在 ,当
,当 时,恒有
时,恒有 .
.
考点:1、导数的应用;2、导数与不等式.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:2015届四川省资阳市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
函数 在[0,3]上的最大值和最小值分别是( ).
在[0,3]上的最大值和最小值分别是( ).
A.5,-15 B.5,-14 C.5,-16 D.5,15
查看答案和解析>>
科目:高中数学 来源:2015届四川省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
已知双曲线 与抛物线
与抛物线 有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若
有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若 , 则此双曲线的离心率等于( ).
, 则此双曲线的离心率等于( ).
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高新区高三9月月考理科数学试卷(解析版) 题型:选择题
将函数 的图象向左平移
的图象向左平移 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
(A)在区间 上单调递减 (B)在区间
上单调递减 (B)在区间 上单调递增
上单调递增
(C)在区间 上单调递减 (D)在区间
上单调递减 (D)在区间 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高新区高三9月月考文科数学试卷(解析版) 题型:选择题
为了研究某药物的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位: )的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,……,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
(A) (B)
(B) (C)
(C) (D)
(D)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com