
分析 设圆柱形铁桶的底面半径为r,则其高h=$\frac{V}{π{r}^{2}}$,记单位面积铁的价格为a,故其总造价y=a(2πr•$\frac{V}{π{r}^{2}}$+πr2)+3aπr2=a($\frac{2V}{π}$+4πr2),求导确定函数的单调性,从而求最小值及最小值点,进一步求其高,则答案可求.
解答 解:设圆柱形铁桶的底面半径为r,则其高为h=$\frac{V}{π{r}^{2}}$.
记单位面积铁的价格为a,
故其总造价y=a(2πr•$\frac{V}{π{r}^{2}}$+πr2)+3aπr2
=a($\frac{2V}{r}$+4πr2),
y′=a(-$\frac{2V}{{r}^{2}}$+8πr)=a$\frac{8π{r}^{3}-2V}{{r}^{2}}$.
故当r∈(0,$\root{3}{\frac{V}{4π}}$)时,y′<0,
当r∈($\root{3}{\frac{V}{4π}}$,+∞)时,y′>0;
故y=a($\frac{2V}{r}$+4πr2)在(0,$\root{3}{\frac{V}{4π}}$)上是减函数,
在($\root{3}{\frac{V}{4π}}$,+∞)上是增函数.
∴当r=$\root{3}{\frac{V}{4π}}$,即其高为h=$\frac{V}{π(\root{3}{\frac{V}{4π}})^{2}}$=$2•\root{3}{\frac{2V}{π}}$时,容器的造价最低,
此时$\frac{r}{h}=\frac{\root{3}{\frac{V}{4π}}}{2•\root{3}{\frac{2V}{π}}}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了导数在实际问题中的应用,同时考查了几何体的表面积的求法,属于中档题.


科目:高中数学 来源: 题型:解答题
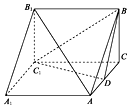 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=2,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=2,D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
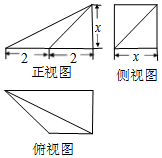
| A. | 3 | B. | 1 | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.4 | B. | 0.6 | C. | 0.8 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com