考点:点、线、面间的距离计算,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)设AB的中点为E,连接EN,证明∠MNE或其补角即为异面直线MN与AC所成的角,连接ME,在Rt△MEN中,可求异面直线MN与AC所成角的大小;
(2)建立空间直角坐标系A-xyz,求出平面ADN的一个法向量,即可求点M到平面ADN之间的距离.
解答:
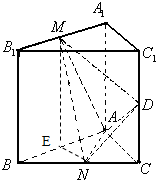
解:(1)设AB的中点为E,连接EN,
则EN∥AC,且
EN=AC,
所以∠MNE或其补角即为异面直线MN与AC所成的角.…3分
连接ME,在Rt△MEN中,
tan∠MNE==2…5分
所以异面直线MN与AC所成的角为arctan2.…6分
(2)因为AB=AC=1,
∠ABC=,所以AB⊥AC,
以点A为坐标原点,分别以AB、AC、AA
1所在直线为x,y,z轴,如图建立空间直角坐标系A-xyz,则:
M(,0,1),
N(,,0),D(0,1,),…8分
设平面AND的一个法向量为
=(x,y,z)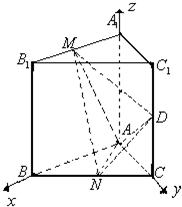
则
⇒所以平面ADN的一个法向量为
=(1,-1,2).…10分
又
=(,0,1),
所以点M到平面OAD的距离
d===.…12分.
点评:本题考查异面直线所成角的大小、考查点M到平面ADN之间的距离,考查向量知识的运用,考查学生的计算能力,属于中档题.

 (理)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC=
(理)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AA1=AB=AC=1,∠ABC= 解:(1)设AB的中点为E,连接EN,
解:(1)设AB的中点为E,连接EN,


