
已知正项数列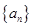 的前
的前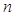 项和为
项和为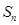 ,且
,且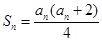
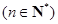 .
.
(1)求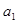 的值及数列
的值及数列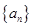 的通项公式;
的通项公式;
(2)求证: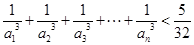
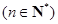 ;
;
(3)是否存在非零整数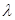 ,使不等式
,使不等式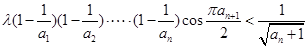
对一切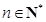 都成立?若存在,求出
都成立?若存在,求出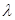 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1) 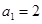 ,
,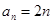
(2)根据题意,由于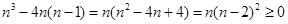 ,∴
,∴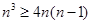 .放缩法来得到证明。
.放缩法来得到证明。
(3)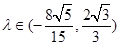 ,由
,由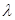 是非零整数,知存在
是非零整数,知存在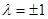 满足条件.
满足条件.
解析试题分析:(1)由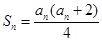 .
.
当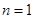 时,
时, ,解得
,解得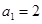 或
或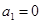 (舍去). 2分
(舍去). 2分
当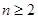 时,
时,
由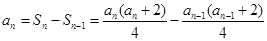
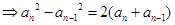 ,
,
∵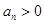 ,∴
,∴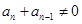 ,则
,则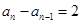 ,
,
∴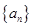 是首项为2,公差为2的等差数列,故
是首项为2,公差为2的等差数列,故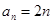 . 4分
. 4分
另法:易得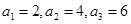 ,猜想
,猜想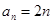 ,再用数学归纳法证明(略).
,再用数学归纳法证明(略).
(2)证法一:∵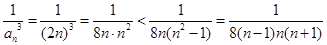
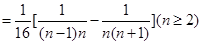 , 4分
, 4分
∴当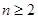 时,
时,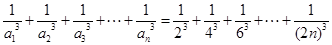
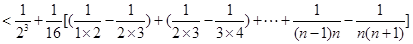
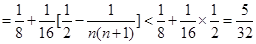 .… 7分
.… 7分
当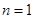 时,不等式左边
时,不等式左边 显然成立. 8分
显然成立. 8分
证法二:∵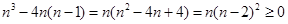 ,∴
,∴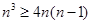 .
.
∴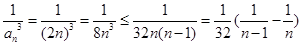
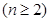 . 4分
. 4分
∴当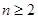 时,
时,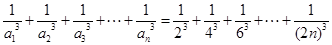
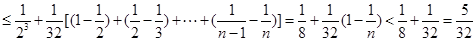 . 7分
. 7分
当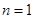 时,不等式左边
时,不等式左边 显然成立. ……8分
显然成立. ……8分
(3)由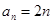 ,得
,得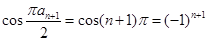 ,
,
设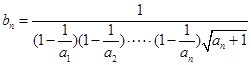 ,则不等式等价于
,则不等式等价于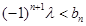 .
.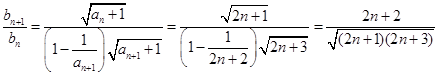
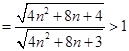 ,……9分
,……9分
∵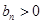 ,∴
,∴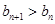 ,数列
,数列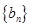 单调递增.
单调递增.
假设存在这样的实数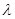 ,使得不等式
,使得不等式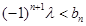 对一切
对一切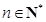 都成立,则
都成立,则
① 当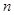 为奇数时,得
为奇数时,得 ; ……11分
; ……11分
② 当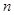 为偶数时,得
为偶数时,得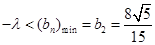 ,即
,即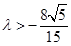 . 12分
. 12分
综上,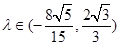 ,由
,由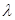 是非零整数,知存在
是非零整数,知存在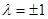 满足条件. 12分
满足条件. 12分
考点:数列与不等式
点评:解决的关键是利用数列的单调性来证明不等式,以及分离参数的思想来求解参数的取值范围。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
下图是一个按照某种规律排列出来的三角形数阵
假设第 行的第二个数为
行的第二个数为
(1)依次写出第六行的所有6个数字(不必说明理由);
(2)写出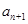 与
与 的递推关系(不必证明),并求出
的递推关系(不必证明),并求出 的通项公式
的通项公式
(3)设 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设数列 的前
的前 项和为
项和为 ,且方程
,且方程 有一个根为
有一个根为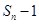 ,
, .
.
(1)证明:数列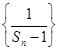 是等差数列;
是等差数列;
(2)设方程 的另一个根为
的另一个根为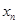 ,数列
,数列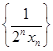 的前
的前 项和为
项和为 ,求
,求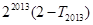 的值;
的值;
(3)是否存在不同的正整数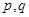 ,使得
,使得 ,
, ,
, 成等比数列,若存在,求出满足条件的
成等比数列,若存在,求出满足条件的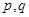 ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列 具有性质:①
具有性质:① 为整数;②对于任意的正整数
为整数;②对于任意的正整数 ,当
,当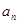 为偶数时,
为偶数时, ;当
;当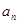 为奇数时,
为奇数时, .
.
(1)若 为偶数,且
为偶数,且 成等差数列,求
成等差数列,求 的值;
的值;
(2)设 (
( 且
且 N),数列
N),数列 的前
的前 项和为
项和为 ,求证:
,求证: ;
;
(3)若 为正整数,求证:当
为正整数,求证:当 (
( N)时,都有
N)时,都有 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{an}和{bn}满足: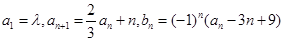 ,其中λ为实数,n为正整数.
,其中λ为实数,n为正整数.
(Ⅰ)若数列{an}前三项成等差数列,求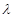 的值;
的值;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com