
����Ŀ������ṩ��ij�����ܽ��ļ�������������ײ�Ʒ�����м�¼�IJ�����![]() �֣�����Ӧ�������ܺ�
�֣�����Ӧ�������ܺ�![]() ���֣���ú�ļ���������ݣ�
���֣���ú�ļ���������ݣ�
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
��1������ݱ����ṩ�����ݣ�����С���˷����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2����֪�ó���������ǰ100�ּײ�Ʒ�ܺ�Ϊ90�ֱ�ú���Ը��ݣ�1����������Իع鷽�̣�Ԥ������100�ּײ�Ʒ�������ܺıȼ�������ǰ���Ͷ��ٶֱ�ú��
���ο�������С���˷������Իع鷽��ϵ����ʽ ��
�� ![]() ��
��
���𰸡���1��![]() ��2��Ԥ������100�ּײ�Ʒ�������ܺıȼ���ǰ����
��2��Ԥ������100�ּײ�Ʒ�������ܺıȼ���ǰ����![]() �֣�
�֣�
����������������� ![]() �����������������������С���˷�����Ҫ�ļ������ݣ�������ϵ��
�����������������������С���˷�����Ҫ�ļ������ݣ�������ϵ��![]() �Ĺ�ʽ����ý�����ٰ��������ĵ���룬���
�Ĺ�ʽ����ý�����ٰ��������ĵ���룬���![]() ֵ���õ����Իع鷽�̣�
ֵ���õ����Իع鷽�̣�
![]() ���ݵ�һ������������Իع鷽�̣���
���ݵ�һ������������Իع鷽�̣���![]() �������Իع鷽�̣����ɵõ��𰸣�
�������Իع鷽�̣����ɵõ��𰸣�
��������1��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
��
����Ļع鷽��Ϊ![]() ��
��
��2��![]() ʱ��
ʱ�� ![]() ���֣���Ԥ������100�ּײ�Ʒ�������ܺıȼ���ǰ����
���֣���Ԥ������100�ּײ�Ʒ�������ܺıȼ���ǰ����![]() ���֣���
���֣���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��ͼ��ʾ���ڶ����� ![]() �У��ı���
�У��ı��� ![]() ��Ϊ�����Σ���
��Ϊ�����Σ���![]() Ϊ
Ϊ ![]() ���е㣬��
���е㣬��![]() ��ƽ�潻
��ƽ�潻 ![]() �� ��
�� ��![]() ��
��
(1) ֤���� ![]() ��
��![]() ��
��
(2) ������![]() ������ֵ��
������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������{An}��{Bn}�ֱ���ij��ǵ���������|AnAn+1|=|An+1An+2|��An��An+1 �� n��N* �� |BnBn+1|=|Bn+1Bn+2|��Bn��Bn+1 �� n��N* �� ��P��Q��ʾ��P��Q���غϣ���dn=|AnBn|��SnΪ��AnBnBn+1�������������
A.{Sn}�ǵȲ�����
B.{Sn2}�ǵȲ�����
C.{dn}�ǵȲ�����
D.{dn2}�ǵȲ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������̨ABC��DEF�У�ƽ��BCFE��ƽ��ABC����ACB=90�㣬BE=EF=FC=1��BC=2��AC=3��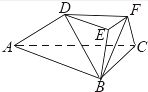
��1����֤��BF��ƽ��ACFD��
��2����ֱ��BD��ƽ��ACFD���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��
��![]() ��һ��ֱ��l��
��һ��ֱ��l��![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() .���㣬
.���㣬![]() ��
��![]() �е㣬l��ֱ��m��
�е㣬l��ֱ��m��![]() �ཻ��
�ཻ��![]() .
.
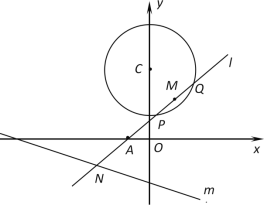
��1����֤����l��m��ֱʱ��l�ع�Բ��![]() ��
��
��2����![]() ʱ����ֱ��l�ķ��̣�
ʱ����ֱ��l�ķ��̣�
��3��̽��![]() �Ƿ���ֱ��l����б���йأ����أ��������ֵ�����йأ���˵������.
�Ƿ���ֱ��l����б���йأ����أ��������ֵ�����йأ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,��ƽ��б����ϵxOy��,��xOy=60��,ƽ��������һ��P����б����ϵ��б���������������:��![]() =xe1+ye2(����e1,e2�ֱ�Ϊx�ᡢy��ͬ����ĵ�λ����),���P��б����Ϊ(x,y).
=xe1+ye2(����e1,e2�ֱ�Ϊx�ᡢy��ͬ����ĵ�λ����),���P��б����Ϊ(x,y).
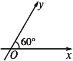
(1)����P��б����ϵxOy�е�б����Ϊ(2,-2),���P��ԭ��O�ľ���.
(2)����ԭ��OΪԲ��,1Ϊ�뾶��Բ��б����ϵxOy�еķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ln��x��1��+ ![]() ��a��R����
��a��R����
��1��������f��x�������䣨1��4���ϵ�����������a��ȡֵ��Χ��
��2��������y=f��x����ͼ����ֱ��4x��3y��2=0���У���a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������д�������������ij��˾������һ������Ͷ�ŵ�ij�ظ�����ʹ�ã�
���г�������ÿ��������Ӫ���ۼ�����y����λ��Ԫ����Ӫ������x![]() ���㺯����ϵ
���㺯����ϵ
ʽ![]() .
.
��1��ҪʹӪ���ۼ��������800Ԫ����Ӫ��������ȡֵ��Χ��
��2��ÿ������Ӫ�˶�����ʱ������ʹÿ���ƽ��Ӫ������![]() ��ֵ���
��ֵ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com