
| A、0个 | B、1个 | C、2个 | D、3个 |


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
| x2 |
| m |
| 3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
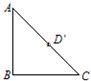 将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )
将一个边长为2的正方形ABCD沿其对角线AC折起,其俯视图如图所示,此时连接顶点B,D形成三棱锥B-ACD,则其正(主)视图的面积为( )| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、直线l1,l2一定有公共点(8,110) |
| B、在两人的回归分析中,小乐求得的线性相关系数r=1,小波求得的线性相关系数r∈(0,1) |
| C、在小乐的回归分析中,他认为x与y之间完全线性相关,所以自己的身高y(cm)与年龄x(岁)成一次函数关系,利用l1可以准确预测自己20岁的身高 |
| D、在小波的回归分析中,他认为x与y之间不完全线性相关,所以自己的身高y(cm)与年龄x(岁)成相关关系,利用l2只可以估计预测自己20岁的身高 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| 2 |
| F1N |
| NF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| x-1 |
| x |
| x-1 |
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com