
分析 (1)利用向量的数量积求解向量的夹角即可.
(2)利用向量的数量积求解$\vec b$在$\vec a$的方向上的投影.
解答 解:(1)向量$\vec a=({2,3})$,$\vec b=({-2,4})$,向量$\vec a$与b夹角为θ,
cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-4+12}{\sqrt{13}\sqrt{20}}$=$\frac{4\sqrt{65}}{65}$;
(2)b在a的方向上的投影为:|$\overrightarrow{b}$|cosθ=2$\sqrt{5}$×$\frac{4\sqrt{65}}{65}$=$\frac{8\sqrt{13}}{13}$.
点评 本题考查平面向量的数量积的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
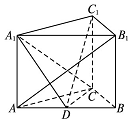 如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3D为AB的中点,AB1⊥A1C
如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3D为AB的中点,AB1⊥A1C查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [(k+$\frac{1}{2}$)π,(k+1)π] | B. | [(2k+1)π,2(k+1)π] | C. | [kπ,(k+$\frac{1}{2}$)π] | D. | [2kπ,(2k+1)π] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:
空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数.空气质量分分级与AQI大小关系如表所示:| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
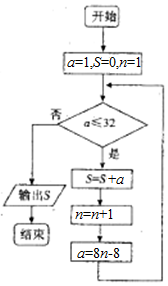 我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )
我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )| A. | 121 | B. | 81 | C. | 74 | D. | 49 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2人 | B. | 3人 | C. | 2人或3人 | D. | 4人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com