
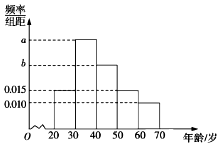
 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.分析 (1)频率分布直方图中,频率=组距×纵坐标及频率和为1,列方程组求解即可;
(2)利用分层抽样原理得出分别抽取的人数,根据抽取情况及代金卷总和为90元,利用古典概型概率公式求解即可.
解答 解:(1)由题意可得$\left\{\begin{array}{l}{a+b=0.060}\\{a+0.015=2b}\end{array}\right.$,
解得a=0.035,b=0.025;
(2)利用分层抽样从样本中抽取5人,
其中年龄在[30,50)为3人,其余年龄段的为2人;
随机抽取3人,有${C}_{5}^{3}$=10种,此3人获得代金券的金额总和为90元,
则需要2个20元和1个50元,有${C}_{3}^{2}$•${C}_{2}^{1}$=6种,
所以此3人获得代金券的金额总和为90元的概率为P=$\frac{6}{10}$=0.6.
点评 本小题主要考查了统计与概率应用问题.也考查了数据处理能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | [1,3) | B. | [$\frac{1}{2}$,3) | C. | [0,4) | D. | [$\frac{1}{2}$,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 2 | C. | -3或2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高一年级 | 7 | 7.5 | 8 | 8.5 | 9 | |||
| 高二年级 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 高三年级 | 6 | 6.5 | 7 | 8.5 | 11 | 13.5 | 17 | 18.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
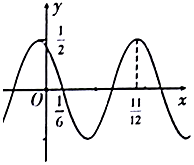
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $-\frac{π}{6}$ | D. | $-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com