
分析 (Ⅰ)求出导函数$f'(x)=\frac{1}{x}-\frac{a}{x^2}$,利用函数f(x)在x=1处的切线平行于直线2x-y=0,列出方程求解即可.
(Ⅱ)求出$f'(x)=\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2}$,若x>1,当a≤1时,当a>1时,分别判断导函数的符号,推出函数的单调性即可.
(Ⅲ)通过当a≤1时,判断是否满足题意;当a>1时,求出f(x)min=f(a)=lna+1,得到lna+1-a≤0,设g(a)=lna+1-a,通过函数的导数利用还是的单调性,转化求解即可.
解答 解:(Ⅰ)∵$f'(x)=\frac{1}{x}-\frac{a}{x^2}$,函数f(x)在x=1处的切线平行于直线2x-y=0,
∴f'(1)=1-a=2,∴a=-1.
(Ⅱ)$f'(x)=\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2}$,若x>1,当a≤1时,f'(x)>0,f(x)在(1,+∞)上单调递增;
当a>1时,f'(x)=0,解得x=a,1<x<a,f'(x)<0;x>a,f'(x)>0,则f(x)在(1,a)上单调递减,在(a,+∞)上单调递增.
(Ⅲ)当a≤1时,f(x)>f(1)=a,则不存在x0∈(1,+∞),使得f(x0)≤a成立,
当a>1时,f(x)min=f(a)=lna+1,
若lna+1≤a,则lna+1-a≤0,设g(a)=lna+1-a,
∴$g'(a)=\frac{1}{a}-1<0$,则g(a)在(1,+∞)单调递减,g(a)<g(1)=0,
∴此时存在x0=a,使得f(x0)≤a成立.
综上所述,a>1.
点评 本题考查函数的导数的应用,切线方程以及函数的最值的求法,考查转化思想以及计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
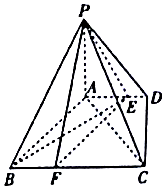 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{2}{3}$ | C. | -1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
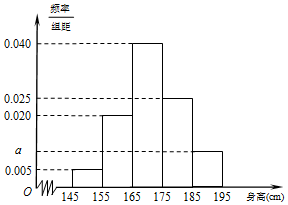 某中学随机选取了40名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
某中学随机选取了40名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com