
分析 利用矩阵的乘法,求出a,d,利用矩阵A的特征多项式为0,求出矩阵A的特征值.
解答 解:因为A$[\begin{array}{l}{1}\\{2}\end{array}]$=$[\begin{array}{l}{a+6}\\{2+2d}\end{array}]$=$[\begin{array}{l}{8}\\{4}\end{array}]$,
所以$\left\{\begin{array}{l}{a+6=8}\\{2+2d=4}\end{array}\right.$,解得a=2,d=1.
所以矩阵A的特征多项式为f(λ)=$|\begin{array}{l}{λ-2}&{-3}\\{-2}&{λ-1}\end{array}|$=(λ-2)(λ-1)-6=(λ-4)(λ+1),
令f(λ)=0,解得矩阵A的特征值为λ=4或-1.
点评 本题考查矩阵的乘法,考查矩阵A的特征值,属于中档题.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2-$\sqrt{2}$] | B. | [2-$\sqrt{2}$,+∞) | C. | (-∞,2-$\sqrt{2}$) | D. | (2-$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
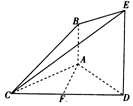 如图,在梯形ADEB中,AB∥DE,AD=DE=2AB,△ACD是正三角形,AB⊥平面ACD,且F是CD的中点.
如图,在梯形ADEB中,AB∥DE,AD=DE=2AB,△ACD是正三角形,AB⊥平面ACD,且F是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com