
分析 运用椭圆的定义可得P也在椭圆$\frac{{y}^{2}}{6}$+$\frac{{x}^{2}}{6-{b}^{2}}$=1上,分别画出两个椭圆的图形,即可判断①正确;
通过b的变化,可得②不正确;由图象可得当P的横坐标和纵坐标的绝对值相等时,|OP|的值取得最小,即可判断③.
解答 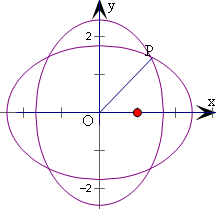 解:椭圆G:$\frac{x^2}{6}+\frac{y^2}{b^2}=1(0<b<\sqrt{6})$的两个焦点分别为
解:椭圆G:$\frac{x^2}{6}+\frac{y^2}{b^2}=1(0<b<\sqrt{6})$的两个焦点分别为
F1($\sqrt{6-{b}^{2}}$,0)和F2(-$\sqrt{6-{b}^{2}}$,0),
短轴的两个端点分别为B1(0,-b)和B2(0,b),
设P(x,y),点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|,
由椭圆定义可得,|PB1|+|PB2|=2a=2$\sqrt{6}$>2b,
即有P在椭圆$\frac{{y}^{2}}{6}$+$\frac{{x}^{2}}{6-{b}^{2}}$=1上.
对于①,将x换为-x方程不变,则点P的轨迹关于y轴对称,
故①正确;
对于②,由图象可得轨迹关于x,y轴对称,且0<b<$\sqrt{6}$,
则椭圆G上满足条件的点P有4个,
不存在b使得椭圆G上满足条件的点P仅有两个,故②不正确;
对于③,由图象可得,当P满足x2=y2,即有6-b2=b2,即b=$\sqrt{3}$时,
|OP|取得最小值,可得x2=y2=2,即有|OP|的最小值为2,故③正确.
故答案为:①③.
点评 本题考查椭圆的定义和方程的运用,以及对称性,考查数形结合的思想方法,以及运算能力,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
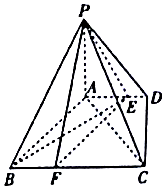 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com