练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知函数f（x）（x∈R）满足f（x）=$\frac{2bx}{ax-1}$，a≠0，f（1）=1且使f（x）=2x成立的实数x只有一个，求函数f（x）的表达式．

    分析 利用f（1）=1，得a=2b+1．根据f（x）=2x只有一解，可得2ax2-2（1+b）x=0（a≠0）只有一解，从而可求b，a的值，即可求函数f（x）的表达式．

    解答 解：由f（1）=1，得a=2b+1．
    由f（x）=2x只有一解，即$\frac{2bx}{ax-1}$=2x，也就是2ax2-2（1+b）x=0（a≠0）只有一解，
    ∴4（1+b）2-4×2a×0=0
    ∴b=-1．
    ∴a=-1．
    故f（x）=$\frac{2x}{x+1}$．

    点评 本题以函数为载体，考查函数的性质，考查函数解析式的求解，正确理解题意是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．在△ABC中，内角A，B，C所对的边分别为a，b，c，若a+b=2，c=1，C=$\frac{π}{3}$，则a=（　　）
    A．$\frac{3}{2}$B．1C．$\frac{\sqrt{3}}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°．
    （1）若$\overrightarrow{a}$，$\overrightarrow{b}$都是单位向量，求|2$\overrightarrow{a}$+$\overrightarrow{b}$|；
    （2）若|$\overrightarrow{a}$|=2，$\overrightarrow{a}$+$\overrightarrow{b}$与2$\overrightarrow{a}$-5$\overrightarrow{b}$垂足，求|$\overrightarrow{b}$|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

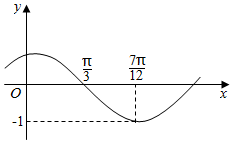
    19．函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，则φ的值为（　　）
    A．$\frac{π}{6}$B．-$\frac{π}{6}$C．$\frac{π}{3}$D．-$\frac{π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知tanx=2，则$\frac{cosx+sinx}{3cosx-sinx}$=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．五一节期间，某商场为吸引顾客消费推出一项优惠活动，活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券．（假定指针等可能地停在任一位置，指针落在区域的边界时，重新转一次）指针所在的区域及对应的返劵金额见表．
    例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．
    （1）已知顾客甲消费后获得n次转动转盘的机会，已知他每转一次转盘指针落在区域边界的概率为p，每次转动转盘的结果相互独立，设ξ为顾客甲转动转盘指针落在区域边界的次数，ξ的数学期望Eξ=$\frac{1}{25}$，方差Dξ=$\frac{99}{2500}$，求n、p的值；
    （2）顾客乙消费280元，并按规则参与了活动，他获得返券的金额记为η（元）．求随机变量η的分布列和数学期望．
    指针位置A区域B区域C区域
    返券金额（单位：元）60300

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．甲、乙两位“准笑星”在“信阳笑星”选拔赛中，5位评委给出的评分情况如图所示，记甲、乙两人的平均得分分别为$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$，记甲、乙两人得分的标准差分别为s1、s2，则下列判断正确的是（　　）
    A．$\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$，s1＜s2B．$\overline{{x}_{甲}}$＜$\overline{{x}_{乙}}$，s1＞s2C．$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$，s1＜s2D．$\overline{{x}_{甲}}$＞$\overline{{x}_{乙}}$，s1＞s2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．cos$\frac{43π}{6}$=（　　）
    A．$\frac{{\sqrt{3}}}{2}$B．$\frac{1}{2}$C．$-\frac{{\sqrt{3}}}{2}$D．$-\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．给出下列命题：
    ①存在实数x，使sinx+cosx=$\frac{3}{2}$；
    ②若α，β是第一象限角，且α＞β，则cosα＜cosβ；
    ③函数y=sin（$\frac{2}{3}$x+$\frac{π}{2}$）是偶函数；
    ④函数y=sin2x的图象向左平移$\frac{π}{4}$个单位，得到函数y=cos2x的图象．
    其中正确命题的序号是③④（把正确命题的序号都填上）

    查看答案和解析>>

    同步练习册答案