练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．抛物线C：y2=16x，C与直线l：y=x-4交于A，B两点，则AB中点到y轴距离为12．

    分析 把直线与抛物线的方程联立，消去y得到一个关于x的一元二次方程，利用根与系数的关系求出两根之和x1+x2，即可求出AB中点到y轴距离．

    解答 解：把直线方程与抛物线方程联立得$\left\{\begin{array}{l}{{y}^{2}=16x}\\{y=x-4}\end{array}\right.$，
    消去y得到x2-24x+16=0，利用根与系数的关系得到x1+x2=24，
    ∴AB中点到y轴距离为12，
    故答案为：12．

    点评 考查学生会求直线与抛物线的交点坐标，灵活运用根与系数的关系及中点坐标公式化简求值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．若不等式x2-2ax+a＞0，对x∈R恒成立，则实数a取值范围为（　　）
    A．{a|1＜a＜2}B．{a|-2＜a＜1}C．{a|0＜a＜2}D．{a|0＜a＜1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．等比数列{an}中，an＞0，a1和a99为方程x2-10x+16=0的两根，则a20•a50•a80的值为64．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．下列说法的正确的是（　　）
    A．经过定点P0（x0，y0）的直线都可以用方程y-y0=k（x-x0）表示
    B．经过定点A（0，b）的直线都可以用方程y=kx+b表示
    C．不经过原点的直线都可以用方程$\frac{x}{a}$+$\frac{y}{b}$=1表示P1（x1，y1）、P2（x2，y2）
    D．经过任意两个不同的点的直线都可以用方程（y-y1）（x2-x1）=（x-x1）（y2-y1）来表示

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=x3+ax2+bx+c在$x=-\frac{2}{3}$与x=1时都取得极值．
    （Ⅰ） 求a，b的值；
    （Ⅱ） 函数f（x）的单调区间及极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．定义：f1（x）=f（x），当n≥2且x∈N*时，fn（x）=f（fn-1（x）），对于函数f（x）定义域内的x0，若正在正整数n是使得fn（x0）=x0成立的最小正整数，则称n是点x0的最小正周期，x0称为f（x）的n～周期点，已知定义在[0，1]上的函数f（x）的图象如图，对于函数f（x），下列说法正确的是①②③（写出所有正确命题的编号）
    ①1是f（x）的一个3～周期点；
    ②3是点$\frac{1}{2}$的最小正周期；
    ③对于任意正整数n，都有fn（${\frac{2}{3}}$）=$\frac{2}{3}$；
    ④若x0∈（$\frac{1}{2}$，1]，则x0是f（x）的一个2～周期点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率为$\frac{1}{2}$，两个焦点恰好在圆O：x2+y2=1上，若过椭圆C左焦点F的直线l与圆O的另一个交点为G，线段FG的中点为M，直线MO交椭圆C于A，B两点，且|AB|=$2\sqrt{2}$|FG|，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．某中学为了解初三年级学生“掷实心球”项目的整体情况，随机抽取男、女生各20名进行测试，记录的数据如下：

    已知该项目评分标准为：
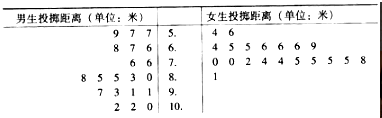
     男生投掷距离（米）…[5.4，6.0）[6.0，6.6）[6.6，7.4）[7.4，7.8）[7.8，8.6）[8.6，10.0）[10.0，+∞）
     
     女生投掷距离（米）    		 
    …    		[5.1，5.4）[5.4，5.6）[5.6，6.4）[6.4，6.8）[6.8，7.2）[7.2，7.6）[7.6，+∞）
     个人得分（分） 
    …    		 4 5 6 7 8 9 10
    注：满分10分，且得9分以上（含9分）定为“优秀”．
    （Ⅰ）求上述20名女生得分的中位数和众数；
    （Ⅱ）从上述20名男生中，随机抽取2名，求抽取的2名男生中优秀人数X的分布列；
    （Ⅲ）根据以上样本数据和你所学的统计知识，试估计该年级学生实心球项目的整体情况．（写出两个结论即可）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．如果a＞0＞b且a+b＞0，那么以下不等式正确的个数是（　　）
    ①a2b＜b3 ②$\frac{1}{a}＞0＞\frac{1}{b}$   ③a3＜ab2 ④a2＞b2．
    A．1B．2C．3D．4

    查看答案和解析>>

    同步练习册答案