练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)=在（1，+∞）上为减函数，则a的取值范围为   （  ）

    A．0<a<         B．0<a≤e          C．a≥e       D．a≤e


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    用0，1，2，3，4这五个数字组成无重复数字的五位数，其中恰有一个偶数数字夹在两个奇数数字之间的五位数的个数是______________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设复数Z满足（Z+i）·Z=1-2i3，则复数Z对应的点位于复平面内   （  ）

    A．第一象限        B．第二象限

    C．第三象限        D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f0(x)=sinx,f1(x)=f’0(x),f2(x)=f’1(x),…,fn+1(x)=f’n(x),n∈N,则f2005(x)    (   )

    A.sinx            B.-sinx         C.cosx       D.-cosx

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(3)=2f’(3)=-2，则的值为    （  ）

    A．-4         B．0       C．8          D．不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     函数f(x)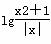＝ (x≠0，x∈R)，有下列命题：

    ①f(x)的图象关于y轴对称；

    ②f(x)的最小值是2；

    ③f(x)在(－∞，0)上是减函数，在(0，＋∞)上是增函数；

    ④f(x)没有最大值．

    其中正确命题的序号是________．(请填上所有正确命题的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ax3＋bx2＋cx，其导函数y＝f′(x)的图象经过点(1,0)，(2,0)，如图所示，则下列说法中不正确的是________．

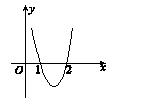
    ①当x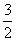＝时，函数f(x)取得极小值；②f(x)有两个极值点；③当x＝2时，函数f(x)取得极小值；④当x＝1时，函数f(x)取得极大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)=xsinx(x∈R)

    (1)证明f(x+2kπ)f(x)=2kπsinx．其中k∈Z；

    (2)设x0是f(x)的一个极值点．证明[f(x0)]2=；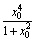

     (3)设f(x)在(0，+∞)的全部极值点按从小到大的顺序a1,a2，…，an，…，证明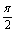：<an+1-an<π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量，n∈N*，且x1＞0.不考虑其它因素，设在第n年内鱼群的繁殖量及捕捞量都与xn成正比，死亡量与xn2成正比，这些比例系数依次为正常数a，b，c.

    （Ⅰ）求xn+1与xn的关系式；

    （Ⅱ）猜测：当且仅当x1，a，b，c满足什么条件时，每年年初鱼群的总量保持不变？（不要求证明）

    （Ⅲ）设a＝2，b＝1，为保证对任意x1∈（0,2），都有xn＞0，n∈N*，则捕捞强度b的最大允许值是多少？证明你的结论.

    查看答案和解析>>

    同步练习册答案