
设函数f(x)=xsinx(x∈R)
(1)证明f(x+2kπ)f(x)=2kπsinx.其中k∈Z;
(2)设x0是f(x)的一个极值点.证明[f(x0)]2=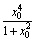 ;
;
(3)设f(x)在(0,+∞)的全部极值点按从小到大的顺序a1,a2,…,an,…,证明: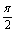 <an+1-an<π.
<an+1-an<π.
 (3)证明:设x0>0是f′(x)=0的任意正实根,即x0-tanx0,则存在一个非负整数k,使x0∈(
(3)证明:设x0>0是f′(x)=0的任意正实根,即x0-tanx0,则存在一个非负整数k,使x0∈(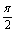 +kπ,π+kπ),即x0在第二或第四象限内.由①式f′(x)=cosx(tanx+x)在第二象限或第四象限中的符号可列表如下:
+kπ,π+kπ),即x0在第二或第四象限内.由①式f′(x)=cosx(tanx+x)在第二象限或第四象限中的符号可列表如下:
| X | ( |
|
| |
| f′(x)的符号 | K为奇数 | - | 0 | + |
| K为偶数 | + | 0 | - |
所以满足f′(x)=0的正根x0都为f(x)的极值点.
由题设条件,a1,a2,…,an…为方程x=-tanx的全部正实根且满足a1<a2<…<an<…那么对于n=1,2,…
an+1-an=-(tanan+ 1-tanan)=-(1+tanan+1·tanan)tan
1-tanan)=-(1+tanan+1·tanan)tan (an+1-an). ②
(an+1-an). ②
由于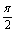 +(n-1)π<an<π+(n-1)π,
+(n-1)π<an<π+(n-1)π,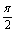 +nπ<an+1<π+nπ,则
+nπ<an+1<π+nπ,则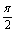 <an+1-an<
<an+1-an<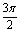 ,由于tanan+1·tanan>0,由②式知tan(an+1-an
,由于tanan+1·tanan>0,由②式知tan(an+1-an )<.0由此可知an+1-an必在第二象限,即an+1-an<π.综上,
)<.0由此可知an+1-an必在第二象限,即an+1-an<π.综上,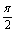 <an+1-an<π
<an+1-an<π


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
函数f(x)= 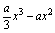 +x+1在x=x1,及x=x2处有极值,且1<
+x+1在x=x1,及x=x2处有极值,且1<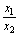 ≤5.
≤5.
(1)求a的取值范围;
(2)当a取最大值时,存在t∈R,使x∈[1,m](m>1)时,f’(t-x) ≤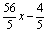 恒成立,试求m的最大值。
恒成立,试求m的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,有一农民在自留地建造一个长10 m,深0.5 m,横截面为等腰梯形的封闭式引水槽侧面材料每平方米造价50元,顶盖材料每平方米造价10元.
(1)把建立引水槽的费用y(元)表示为引水槽的侧面与地面所成的角∠DAE=θ的函数;
(2)引水槽的侧面与地面所成的角θ多大时,其材料费最低?最低材料费是多少?(精确到0.01,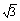 ≈1.732)
≈1.732)
(3)按照题没条件,在引水槽的深度和横截面积及所在的材料不改变的情况下,将引水槽的横截面形状改变为正方形时的材料费与(2)中所求得的材料费相比较,哪一种设计所用材料费更省?省多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com