
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | 4 |
分析 由圆的方程找出圆心与半径,判断得到(3,1)在圆内,过此点最短的弦即为与过此点直径垂直的弦,利用垂径定理及勾股定理即可求出.
解答 解:由圆的标准方程得圆心(2,2),半径r=2,
∵$\sqrt{({3-2)}^{2}+({1-2)}^{2}}$=$\sqrt{2}$<2,∴(3,1)在圆内,
∵圆心到此点的距离d=$\sqrt{2}$,r=2,
∴最短的弦长为2$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{2}$.
故选:B.
点评 本题主要考查直线和圆相交的弦长的计算,涉及的知识有:圆的标准方程,点与圆的位置关系,垂径定理,以及勾股定理,找出最短弦是解本题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
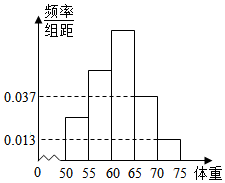 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<e<$\frac{1}{5}$ | B. | $\frac{1}{5}$<e<$\frac{1}{3}$ | C. | $\frac{1}{3}$<e<1 | D. | 0<e<$\frac{1}{5}$或$\frac{1}{3}$<e<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 语文(x分) | 89 | 91 | 93 | 95 | 97 |
| 英语(y分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com