
���� ��1����a=11ʱ�������B���7λ���˿���ʱ���ƽ�������ɴ������B���7λ���˿���ʱ��ķ��
��2������֪��X�Ŀ���ȡֵΪ0��1��2��3��4���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�EX��
��� �⣺��1����a=11ʱ��B���7λ���˿���ʱ���ƽ������
$\overline{x}$=$\frac{1}{7}$��12+13+15+16+17+14+11��=14��
B���7λ���˿���ʱ��ķ��
S2=$\frac{1}{7}$[��12-14��2+��13-14��2+��15-14��2+��16-14��2+��17-14��2+��14-14��2+��11-14��2=4��
��2����a=14��������ҵĿ���ʱ�䶼����15��
�Ŀ���ʱ�����ҵĿ���ʱ��IJ�ľ���ֵX��
��X�Ŀ���ȡֵΪ0��1��2��3��4��
P��X=0��=$\frac{1}{5}��\frac{1}{2}$+$\frac{1}{4}��\frac{1}{5}+\frac{1}{4}��\frac{1}{5}$=$\frac{1}{5}$��
P��X=1��=$\frac{1}{5}��\frac{1}{2}$+$\frac{1}{5}��\frac{1}{4}$+$\frac{1}{4}��\frac{1}{5}+$$\frac{1}{5}��\frac{1}{2}$=$\frac{3}{10}$��
P��X=2��=$\frac{1}{5}��\frac{1}{4}$+$\frac{1}{5}��\frac{1}{4}$+$\frac{1}{5}��\frac{1}{4}$+$\frac{1}{5}��\frac{1}{2}$=$\frac{1}{4}$��
P��X=3��=$\frac{1}{5}��\frac{1}{4}+\frac{1}{5}��\frac{1}{2}$=$\frac{3}{20}$��
P��X=4��=$\frac{1}{5}��\frac{1}{2}$=$\frac{1}{10}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{5}$ | $\frac{3}{10}$ | $\frac{1}{4}$ | $\frac{3}{20}$ | $\frac{1}{10}$ |
���� ���⿼�鷽�����������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע��������¼��˷���ʽ�ĺ������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
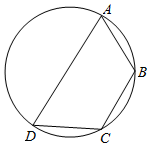 ��ͼ����֪�ı���ABCD��Բ�ڽ��ı��Σ��ҡ�BCD=120�㣬AD=2��AB=BC=1������ı��ε�������ڣ�������
��ͼ����֪�ı���ABCD��Բ�ڽ��ı��Σ��ҡ�BCD=120�㣬AD=2��AB=BC=1������ı��ε�������ڣ�������| A�� | $\sqrt{3}$ | B�� | $\frac{3\sqrt{3}}{4}$ | C�� | $\sqrt{3}$+1 | D�� | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��m�Φ���n�Φ�����m��n | B�� | ��m�ͦ���n�Φ£����ͦ£���m��n | ||
| C�� | �����ɦ�=l��m�Φ���m�Φ£���m��l | D�� | �����ɦ�=m�����ɦ�=n��l��m��l��n����l�ͦ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $2\sqrt{2}$ | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����� | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 181 | 166 | 185 | 180 |
| y | 95 | 100 | 97 | 103 | 101 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪F1��F2����ԲC�����ҽ��㣬��A��BΪ�����Ҷ��㣬PΪ��ԲC�ϣ�����A��B����һ���㣬��P������Ϊ��1��$\frac{3}{2}$��ʱ����PF1F2�����Ϊ$\frac{3}{2}$���ֱ����A��B��P����ԲC������l1��l2��l��ֱ��l��l1��l2�ֱ��ڵ�R��T��
��֪F1��F2����ԲC�����ҽ��㣬��A��BΪ�����Ҷ��㣬PΪ��ԲC�ϣ�����A��B����һ���㣬��P������Ϊ��1��$\frac{3}{2}$��ʱ����PF1F2�����Ϊ$\frac{3}{2}$���ֱ����A��B��P����ԲC������l1��l2��l��ֱ��l��l1��l2�ֱ��ڵ�R��T���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��֪��Բ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����ԲO��x2+y2=a2����ͼ����B��0��a������Բ���е�ֱ��l��ԲO�ڵ�A������AOB=60�㣬����Բ��������Ϊ��������
��֪��Բ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����ԲO��x2+y2=a2����ͼ����B��0��a������Բ���е�ֱ��l��ԲO�ڵ�A������AOB=60�㣬����Բ��������Ϊ��������| A�� | $\frac{\sqrt{3}}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{2}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com